题目内容
17．
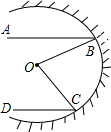如图是汽车灯的剖面图，从O点发出的光纤照射到凹面镜上，反射出的光线BA、CD是互相平行的水平线，若∠DCO=50°，∠ABD=α，则∠BOC的度数为50°+α（用含α的式子表示）．
分析 连接BC，由AB∥CD可以推出∠ABO+∠CBO+∠BCO+∠OCD=180°，而∠CBO+∠BCO+∠0=180°，由此可以证明∠0=∠ABO+∠DCO．
解答 
解：连接BC，
∵AB∥CD，
∴∠ABO+∠CBO+∠BCO+∠OCD=180°，
而∠CBO+∠BCO+∠0=180°，
∴∠0=∠ABO+∠DCO=50°+α．
故填空答案：50°+α．
点评 此题考查平行线的性质，关键是根据三角形的内角和是180°以及平行线的性质：两直线平行，同旁内角互补分析．
练习册系列答案
相关题目
7．
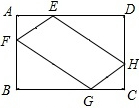如图，在矩形ABCD中，AB=5，BC=6，点E，F，G，H分别在已知矩形的四条边上，且四边形EFGH也是矩形，GF=2EF．若设AE=a，AF=b，则a与b满足的关系为（ ）
如图，在矩形ABCD中，AB=5，BC=6，点E，F，G，H分别在已知矩形的四条边上，且四边形EFGH也是矩形，GF=2EF．若设AE=a，AF=b，则a与b满足的关系为（ ）| A． | $\left\{\begin{array}{l}{a+b=5}\\{a+2b=6}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{a=2b}\\{2a+b=6}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{2a+b=5}\\{a+2b=6}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{2a+b=6}\\{a+2b=5}\end{array}\right.$ |
（1）计算：（-3）0-$\sqrt{27}$+|1-$\sqrt{2}$|+$\frac{1}{\sqrt{3}+\sqrt{2}}$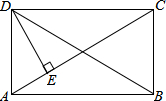
如图，在矩形ABCD中，DE⊥AC，∠ADE=$\frac{1}{2}$∠CDE，那么∠BDC的度数为30°．