题目内容
2.若$\sqrt{x}$+$\sqrt{\frac{1}{x}}$=$\sqrt{6}$,x≥1,则$\sqrt{x}$-$\sqrt{\frac{1}{x}}$=( )| A. | ±2 | B. | -$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | $±\sqrt{2}$ |
分析 把$\sqrt{x}$+$\sqrt{\frac{1}{x}}$=$\sqrt{6}$两边平方求得x+$\frac{1}{x}$的值,然后求得($\sqrt{x}$-$\sqrt{\frac{1}{x}}$)2的值,然后开方即可.
解答 解:∵$\sqrt{x}$+$\sqrt{\frac{1}{x}}$=$\sqrt{6}$,
∴($\sqrt{x}$+$\sqrt{\frac{1}{x}}$)2=6,即x+$\frac{1}{x}$+2=6,
∴x+$\frac{1}{x}$=4,
∴($\sqrt{x}$-$\sqrt{\frac{1}{x}}$)2=x+$\frac{1}{x}$-2=4-2=2,
又∵x≥1,
∴$\sqrt{x}$-$\sqrt{\frac{1}{x}}$≥0,
∴$\sqrt{x}$-$\sqrt{\frac{1}{x}}$=$\sqrt{2}$.
故选C.
点评 本题考查了二次根式的化简求值,理解完全平方公式的结构,根据已知求得($\sqrt{x}$-$\sqrt{\frac{1}{x}}$)2的值是关键.

练习册系列答案
相关题目
10.如果方程2x-6=0,那么3x+8的值( )
| A. | 11 | B. | 14 | C. | 17 | D. | 20 |
14.下列说法中不正确的是( )
| A. | 在平面内,两条互相垂直、原点重合的数轴的垂足是原点 | |
| B. | 平面直角坐标系所在平面叫坐标平面 | |
| C. | 坐标平面上的点与有序数对是一一对应的 | |
| D. | 凡是两条互相垂直的直线都能组成平面直角坐标系 |
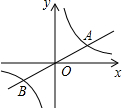 已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于A、B两点,且点A的横坐标为4.
已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于A、B两点,且点A的横坐标为4.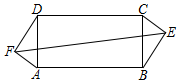 矩形ABCD中,AD=5,AB=10,E、F分别为矩形外的两点,BE=DF=4,AF=CE=3,则EF=$\sqrt{221}$.
矩形ABCD中,AD=5,AB=10,E、F分别为矩形外的两点,BE=DF=4,AF=CE=3,则EF=$\sqrt{221}$.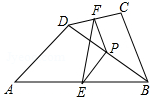 如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是120°.
如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是120°.