题目内容
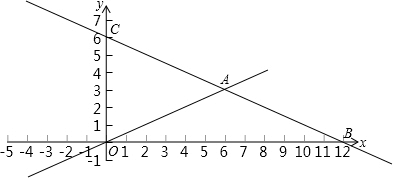
已知直线y=x+4的图象与x轴、y轴交于A、B两点,直线L经过原点,与线段AB交于点C,且把△AOB的面积分成2:1的两部分,则直线L的解析式为 .
考点:一次函数图象上点的坐标特征
专题:
分析:根据直线y=x+4的解析式可求出A、B两点的坐标,如图:
(1)当直线l把△ABO的面积分为S△AOC:S△BOC=2:1时,作CF⊥OA于F,CE⊥OB于E,可分别求出△AOB与△AOC的面积,再根据其面积公式可求出两直线交点的坐标,从而求出其解析式;
(2)当直线l把△ABO的面积分为S△AOC:S△BOC=1:2时,同(1).
(1)当直线l把△ABO的面积分为S△AOC:S△BOC=2:1时,作CF⊥OA于F,CE⊥OB于E,可分别求出△AOB与△AOC的面积,再根据其面积公式可求出两直线交点的坐标,从而求出其解析式;
(2)当直线l把△ABO的面积分为S△AOC:S△BOC=1:2时,同(1).
解答: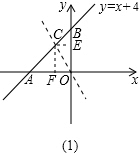 解:由直线y=x+4的解析式可求得A(-4,O)、B(0,4),
解:由直线y=x+4的解析式可求得A(-4,O)、B(0,4),
如图(1),当直线l把△AOB的面积分为S△AOC:S△BOC=2:1时,
作CF⊥OA于F,CE⊥OB于E,则S△AOB=8,则S△AOC=
,
∴
AO•CF=
,即
×4×CF=
,
∴CF=
.
同理,解得CE=
.
 ∴C(-
∴C(-
,
),
∴直线l的解析式为y=-2x;
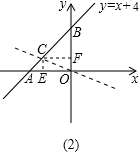
如图(2),当直线l把△ABO的面积分为S△AOC:S△BOC=1:2时,
同理求得C(-
,
),
∴直线l的解析式为y=-
x.
故答案为y=-2x或y=-
x.
 解:由直线y=x+4的解析式可求得A(-4,O)、B(0,4),
解:由直线y=x+4的解析式可求得A(-4,O)、B(0,4),如图(1),当直线l把△AOB的面积分为S△AOC:S△BOC=2:1时,
作CF⊥OA于F,CE⊥OB于E,则S△AOB=8,则S△AOC=
| 16 |
| 3 |
∴
| 1 |
| 2 |
| 16 |
| 3 |
| 1 |
| 2 |
| 16 |
| 3 |
∴CF=
| 8 |
| 3 |
同理,解得CE=
| 4 |
| 3 |
 ∴C(-
∴C(-| 4 |
| 3 |
| 8 |
| 3 |
∴直线l的解析式为y=-2x;
如图(2),当直线l把△ABO的面积分为S△AOC:S△BOC=1:2时,
同理求得C(-
| 8 |
| 3 |
| 4 |
| 3 |
∴直线l的解析式为y=-
| 1 |
| 2 |
故答案为y=-2x或y=-
| 1 |
| 2 |
点评:此题考查的是用待定系数法求一次函数的解析式,涉及到三角形的面积公式及分类讨论的方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
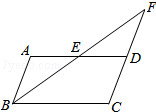 如图,在?ABCD中,E是AD边上的中点,连接BE,并延长BE交CD延长线于点F,则△ABE与△BCF的面积之比是( )
如图,在?ABCD中,E是AD边上的中点,连接BE,并延长BE交CD延长线于点F,则△ABE与△BCF的面积之比是( )| A、1:2 | B、1:3 |
| C、1:4 | D、1:5 |