题目内容
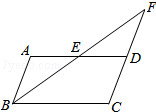如图，在?ABCD中，E是AD边上的中点，连接BE，并延长BE交CD延长线于点F，则△ABE与△BCF的面积之比是（ ）| A、1：2 | B、1：3 |
| C、1：4 | D、1：5 |
考点：平行四边形的性质,全等三角形的判定与性质
专题：
分析：由四边形ABCD是平行四边形，易证得△ABE∽△DFE，△DFE∽△CFB，则可得△ABE∽△CFB，又由E是AD边上的中点，根据相似三角形的面积比等于相似比的平方，即可求得答案．
解答：解：∵四边形ABCD是平行四边形，
∴AB∥CD，AD∥BC，AD=BC，
∴△ABE∽△DFE，△DFE∽△CFB，
∴△ABE∽△CFB，
∵E是AD边上的中点，
∴AB：DF=AE：DE=1，
∴AB=DF=CD，
∴AB：CF=1：2，
∴△ABE与△BCF的面积之比是：1：4．
故选C．
∴AB∥CD，AD∥BC，AD=BC，
∴△ABE∽△DFE，△DFE∽△CFB，
∴△ABE∽△CFB，
∵E是AD边上的中点，
∴AB：DF=AE：DE=1，
∴AB=DF=CD，
∴AB：CF=1：2，
∴△ABE与△BCF的面积之比是：1：4．
故选C．
点评：此题考查了平行四边形的性质以及相似三角形的判定与性质．此题难度适中，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
如图1，AD平分△ABC的外角∠EAC，且AD∥BC，若∠BAC=80°，则∠B=如图中是一个几何体的主视图、左视图、俯视图，则它们对应的几何体是（ ）
A、 |
B、 |
C、 |
D、 |
下列选项中，能写成反比例函数的是（ ）
| A、人的体重和身高 |
| B、正三角形的边长和面积 |
| C、速度一定，路程和时间的关系 |
| D、销售总价不变，销售单价与销售数量的关系 |
一组数据：-1、0、1、2、3，则平均数和中位数分别是（ ）
| A、1，0 | B、2，1 |
| C、1，2 | D、1，1 |
当a是偶数时，（x-y）a•（y-x）b与（y-x）a+b的关系是（ ）
| A、相等 | B、互为倒数 |
| C、互为相反数 | D、无法确定 |
下列运算中，错误的有（ ）
①
=1
，②
=±4，③
=2，④
=
+
=
．
①
1
|
| 5 |
| 12 |
| 42 |
| (-2)2 |
|
| 1 |
| 4 |
| 1 |
| 5 |
| 9 |
| 20 |
| A、1个 | B、2个 | C、3个 | D、4个 |