题目内容
19．已知⊙O的半径为5cm，P为该圆内一点，且OP=1cm，则过点P的弦中，最短的弦长为（ ）| A． | 8cm | B． | 6cm | C． | 4$\sqrt{6}$cm | D． | 4$\sqrt{3}$cm |
分析 根据勾股定理和垂径定理即可求得．
解答 
解：在过点P的所有⊙O的弦中，最短的弦长为垂直于OP的弦，即OP⊥AB，
连接OA，
在RT△AOP中，OA=5cm．OP=1cm．根据勾股定理可得：AP=2$\sqrt{6}$cm，
根据垂径定理可得：AB=2AP，
所以AB=4$\sqrt{6}$cm．
故选C．
点评 本题考查了综合运用垂径定理和勾股定理进行计算，此题关键是能够正确分析出其最短的弦．
练习册系列答案
相关题目
10．
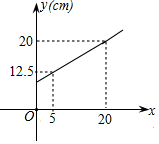弹簧的长度y（cm）与所挂物体的质量x（kg）的关系是一次函数，图象如图所示，则弹簧不挂物体时的长度是（ ）
弹簧的长度y（cm）与所挂物体的质量x（kg）的关系是一次函数，图象如图所示，则弹簧不挂物体时的长度是（ ）| A． | 9cm | B． | 10cm | C． | 10.5cm | D． | 11cm |
一条排水管的截面如图所示．已知排水管的半径OB=10，水面宽AB=16．求截面圆心O到水面的距离．
14．已知二次函数y=x2+2x+2，图象的顶点为A，图象与y轴交于点B，O为坐标原点，则AB的长等于（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | $\sqrt{5}$ |
4．单项式-$\frac{{2}^{3}{a}^{2}b}{5}$的次数是（ ）
| A． | -23 | B． | -$\frac{8}{5}$ | C． | 6 | D． | 3 |