��Ŀ����
10�����壺y��һ������x�ĺ�����������ÿ��ʵ��x������y��ֵΪ����x+2��2x+1��-5x+20�е���Сֵ������y��������������Сֵ��������1�����������Сֵ������ͼ���жϵ�A��1��3���Ƿ�Ϊ�����Сֵ����ͼ���ϵĵ㣻
��2���������Сֵ����ͼ�����ߵ�ΪB����A��1��3��������M��m��m��
��ֱ��д����ABM��������������2��
������MΪԲ�ĵ�Բ����A��B���㣬д����M�����ꣻ
���Ԣ��еĵ�MΪԲ�ģ���$\sqrt{2}$Ϊ�뾶��Բ���ڴ�Բ����һ��P��ʹPA+$\frac{\sqrt{2}}{2}$PB��ֵ��С��ֱ��д������Сֵ��
���� ��1��������������Сֵ�����Ķ��廭��ͼ�ɣ�����ͼ������жϵ�A��λ�ã�
��2������ͼ2�У���ON��AB��N����AB��OM����S��ABM=S��ABO�ɴ˼����жϣ�
������߶�AB���д��ߣ����г������鼴�ɽ�����⣮
����ͼ3�У�ȡBM���е�D������PD��PM����PM2=2=1��2=MD•BM���Ƴ���PMD�ס�BMP���Ƴ�$\frac{PD}{PB}$=$\frac{MD}{PM}$=$\frac{\sqrt{2}}{2}$��
�Ƴ�PD=$\frac{\sqrt{2}}{2}$PB���Ƴ�PA+$\frac{\sqrt{2}}{2}$PB=PA+PD��AD���Ƴ����ɽ�����⣮
��� �⣺��1����Сֵ������ͼ���ͼ��ʵ�ߣ�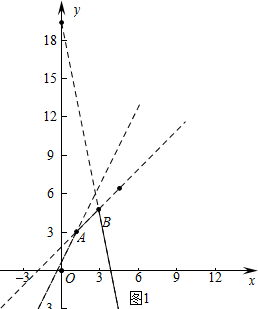
��x=1ʱ��y=3��
���A��1��3���������Сֵ������ͼ���ϣ�
��2������ͼ2�У���ON��AB��N��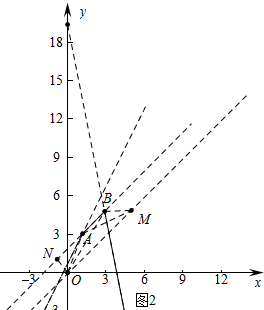
��AB��OM��
��S��ABM=S��ABO��
��A��1��3����B��3��5����ON=$\sqrt{2}$��AB=2$\sqrt{2}$
��S��ABM=$\frac{1}{2}$��$2\sqrt{2}$��$\sqrt{2}$=2��
�ʴ�Ϊ2��
�ڡ�ֱ��AB�Ľ���ʽΪy=x+2��
���߶�AB���д��ߵĽ���ʽΪy=-x+6��
��$\left\{\begin{array}{l}{y=-x+6}\\{y=x}\end{array}\right.$���$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$��
���M������3��3����
����ͼ3�У�ȡBM���е�D������PD��PM��
��PM2=2=1��2=MD•BM��
�ߡ�PMD=��BMP��
���PMD�ס�BMP��
��$\frac{PD}{PB}$=$\frac{MD}{PM}$=$\frac{\sqrt{2}}{2}$��
��PD=$\frac{\sqrt{2}}{2}$PB��
��PA+$\frac{\sqrt{2}}{2}$PB=PA+PD��AD��
��AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=5��
��PA+$\frac{\sqrt{2}}{2}$PB��5��
��PA+$\frac{\sqrt{2}}{2}$PB����СֵΪ5��
���� ���⿼��Բ���ۺ��⡢һ�κ�����ƽ���ߵ����ʡ����������ε��ж������ʵ�֪ʶ������Ĺؼ����������⣬��ȷ����ͼ�Σ�ѧ��ת����˼�룬���������ν�ϵ�˼�룬�����п�ѹ���⣮

| A�� | 24Ԫ | B�� | 26Ԫ | C�� | 28Ԫ | D�� | 30Ԫ |
| A�� | -5 | B�� | 1 | C�� | -1 | D�� | -6 |
| A�� | 2��x2-y2�� | B�� | 2��x+y����x-y�� | C�� | 2��x+y��2 | D�� | 2��x-y��2 |
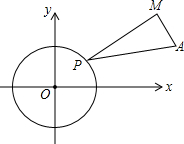 ��ͼ����O����ԭ��ΪԲ�ģ��뾶Ϊ2��Բ����A��6��2������P�ǡ�O��һ���㣬���߶�PAΪб�߹���ֱ�ǡ�PAM����cos��MPA=$\frac{2\sqrt{2}}{3}$������֪����P�ڡ�O���˶�ʱ�����֡�MPA�Ĵ�С���䣬��M���ŵ�P�˶����˶����˶�·��Ҳ�γ�һ��Բ�����Բ�İ뾶�ǣ�������
��ͼ����O����ԭ��ΪԲ�ģ��뾶Ϊ2��Բ����A��6��2������P�ǡ�O��һ���㣬���߶�PAΪб�߹���ֱ�ǡ�PAM����cos��MPA=$\frac{2\sqrt{2}}{3}$������֪����P�ڡ�O���˶�ʱ�����֡�MPA�Ĵ�С���䣬��M���ŵ�P�˶����˶����˶�·��Ҳ�γ�һ��Բ�����Բ�İ뾶�ǣ�������| A�� | $\frac{1}{3}$ | B�� | $\frac{2\sqrt{2}}{3}$ | C�� | $\frac{2}{3}$ | D�� | 1 |
| A�� | x2+x3=2x5 | B�� | m8��m2=m4 | C�� | ��m-n��2=m2-n2 | D�� | ��x2��3=x6 |

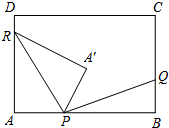 ��ͼ���ھ���ABCD�У�AB=8k��BC=5k��kΪ��������k��0��������P��AB���ϣ���P����A��B�غϣ�����Q��R�ֱ���BC��DA���ϣ���AP��BQ��DR=3��2��1����A����ֱ��PR�ĶԳƵ�ΪA�䣬����PA�䡢RA�䡢PQ��
��ͼ���ھ���ABCD�У�AB=8k��BC=5k��kΪ��������k��0��������P��AB���ϣ���P����A��B�غϣ�����Q��R�ֱ���BC��DA���ϣ���AP��BQ��DR=3��2��1����A����ֱ��PR�ĶԳƵ�ΪA�䣬����PA�䡢RA�䡢PQ��