题目内容
14. 已知:如图,在数轴上,点A表示的数为10,点B表示的数为13,点M丧示的数是-20.求:
已知:如图,在数轴上,点A表示的数为10,点B表示的数为13,点M丧示的数是-20.求:(1)线段AB的长为3单位长度;
(2)若线段AB以1单位长度/秒的速度匀速向左运动,同时,点M以2单位长度/秒的速度沿数轴向右匀速运动,设运动时间为t秒.
①当点A与原点O重合时,t的值为10;
②是否存在某一时刻t,MA=2BO?若存在,请求出此时t的值;不存在,说明理由.
分析 (1)利用两点之间的距离求得AB之间的距离即可;
(2)①利用A点运动的距离是OA的长度列出方程解答即可;
②用t表示出MA、BO的长度,利用MA=2BO列出方程解答即可.
解答 解:(1)线段AB的长为13-10=3单位长度;
(2)①由题意得t=10;
②MA=10-(-20)=30,BO=13,
由题意得
30-(2+1)t=2(13-t)
解得:t=4
所以当t=4时,MA=2BO.
点评 此题考查一元一次方程的实际运用,掌握两点之间的距离求法以及行程问题中的基本数量关系是解决问题的关键.

练习册系列答案
相关题目
3.三角形的角平分线、中线和高( )
| A. | 都是射线 | B. | 都是直线 | C. | 都是线段 | D. | 都在三角形内 |
 如图是一个圆台及其主视图,你能把它的俯视图和左视图补上吗?
如图是一个圆台及其主视图,你能把它的俯视图和左视图补上吗?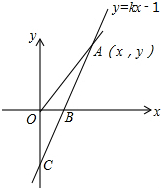 如图,直线y=kx-1与x轴、y轴分别交于B、C两点,且OC=2OB.
如图,直线y=kx-1与x轴、y轴分别交于B、C两点,且OC=2OB.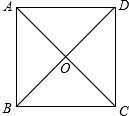 下面的判断是否正确.说明理由:
下面的判断是否正确.说明理由: