题目内容
7.已知甲、乙两人均从400米的环形跑道的A处出发,各自以每秒6米和每秒8米的速度在跑道上跑步.(1)若两人同时出发,背向而行,则经过$\frac{200}{7}$秒钟两人第一次相遇;若两人同时出发,同向而行,则经过200秒钟乙第一次追上甲.
(2)若两人同向而行,乙在甲出发10秒钟后去追甲,经过多少时间乙第二次追上甲.
(3)若让甲先跑10秒钟后乙开始跑,在乙用时不超过100秒的情况下,乙跑多少秒钟时,两人相距40米.
分析 (1)根据时间=路程÷速度之和即可算出(背向而行时)经过多久两人第一次相遇;再根据时间=路程÷速度之差即可算出(同向而行时)经过多久两人第一次相遇;
(2)设经过x秒时乙第二次追上甲,根据乙跑过的路程-甲跑过的路程=跑道一圈的长度+甲提前跑的长度即可得出关于x的一元一次方程,解之即可得出结论;
(3)设经过y秒时甲乙两人相距40米,分两人同向而行和背向而行两种情况考虑,根据二者间的距离即可得出关于y的一元一次方程,解之即可得出结论.
解答 解:(1)400÷(6+8)=$\frac{200}{7}$(秒);
400÷(8-6)=200(秒).
故答案为:$\frac{200}{7}$;200.
(2)设经过x秒时乙第二次追上甲,
根据题意得:8x-6x=400+6×10,
解得:x=230.
答:经过230秒钟乙第二次追上甲.
(3)设经过y秒时甲乙两人相距40米,
甲、乙同向而行时,|6(10+y)-8y|=40,
解得:y=10或y=50;
甲、乙背向而行时,6(10+y)+8y=400n-40或6(10+y)+8y=400n+40;
解得:y=$\frac{200n-50}{7}$或y=$\frac{200n-10}{7}$,
∵y≤100,
∴y=$\frac{150}{7}$、$\frac{190}{7}$、50、$\frac{390}{7}$、$\frac{550}{7}$、$\frac{590}{7}$.
答:当甲、乙同向而行时,乙跑10秒或50秒时,两人相距40米;当甲、乙背向而行时,乙跑$\frac{150}{7}$、$\frac{190}{7}$、50、$\frac{390}{7}$、$\frac{550}{7}$或$\frac{590}{7}$秒时,两人相距40米.
点评 本题考查了一元一次方程的应用,解题的关键是:(1)根据时间=路程÷速度列式计算;(2)根据路程=速度×时间结合甲、乙跑过的路程差列出关于x的一元一次方程;(3)分两人同向而行和背向而行两种情况考虑.

 阅读快车系列答案
阅读快车系列答案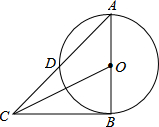 如图,AB是⊙O直径,AD是弦,过B点的切线与AD的延长线交于点C,若AD=CD,求sin∠OCA的值.
如图,AB是⊙O直径,AD是弦,过B点的切线与AD的延长线交于点C,若AD=CD,求sin∠OCA的值.
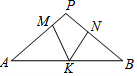 如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=43°,则∠P的度数为94度.
如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=43°,则∠P的度数为94度.