题目内容
已知CD是⊙O的直径,AB是弦,AB⊥CD于点M,若CD=20,OM:OC=3:5,求弦AB的长.
考点:垂径定理,勾股定理
专题:
分析:连接OA,先根据⊙O的直径CD=20得出OC的长,再根据OM:OC=3:5求出OM的长,在Rt△AOM中根据勾股定理即可得出AM的长,进而可得出结论.
解答:解:连接OA,
∵CD是⊙O的直径,
∴OD=OC=10,
又∵OM:OC=3:5,
∴OM=6,
在Rt△AOM中,由勾股定理得,AM=
=8,
故AB=2AM=16.

∵CD是⊙O的直径,
∴OD=OC=10,
又∵OM:OC=3:5,
∴OM=6,
在Rt△AOM中,由勾股定理得,AM=
| AO2-OM2 |
故AB=2AM=16.
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.

练习册系列答案
相关题目
已知点A的坐标为(3,4),O为原点,连结OA,将线段OA绕点O按逆时针方向旋转90°得OA1,则点A1的坐标为( )
| A、(-3,4) |
| B、(3,-4) |
| C、(-4,3) |
| D、(4,-3) |
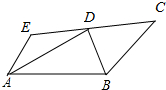 已知,如图,AE∥BC,AD、BD分别平分∠EAB、∠CBA,EC过点D.求证:AB=AE+BC.
已知,如图,AE∥BC,AD、BD分别平分∠EAB、∠CBA,EC过点D.求证:AB=AE+BC.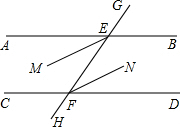 如图,已知直线AB和直线CD被直线GH所截,交点分别为E,F,∠AEF=∠EFD.
如图,已知直线AB和直线CD被直线GH所截,交点分别为E,F,∠AEF=∠EFD. 如图,AB=AC+
如图,AB=AC+