题目内容
11. 已知:如图,?ABCD中,CD=CB=2,∠C=60°,点E是CD边上自D向C的动点(点E运动到点C停止运动),连结AE,以AE为一边作等边△AEP,连结DP.
已知:如图,?ABCD中,CD=CB=2,∠C=60°,点E是CD边上自D向C的动点(点E运动到点C停止运动),连结AE,以AE为一边作等边△AEP,连结DP.(1)求证:△ABE≌△ADP;
(2)点P随点E的运动而运动,请直接写出点P的运动路径长2.
分析 (1)根据平行四边形、菱形、等边三角形的性质得到AP=AE,∠PAE=60°,∠PAE=∠DAB,∠1=∠2,从而得到全等三角形;
(2)根据点E的运动路径长是2,得到点P的运动路径长是2.
解答 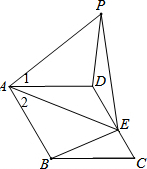 (1)证明:在?ABCD中,
(1)证明:在?ABCD中,
∵BC=CD,
∴?ABCD是菱形,
∴AB=AD,
∵△AEP是等边三角形,
∴AP=AE,∠PAE=60°,
∵∠BAD=∠C=60°,
∴∠PAE=∠DAB,
∴∠PAE-∠DAE=∠DAB-∠DAE,
即∠1=∠2,
在△ABE与△ADP中,
$\left\{\begin{array}{l}{AP=AE}\\{∠1=∠2}\\{AD=AB}\end{array}\right.$,
∴△ABE≌△ADP(SAS);
(2)解:∵点E在CD边上自D向C的运动,
∴点E的运动路径长是2,
∴点P的运动路径长为:2.
故答案为:2.
点评 本题考查了全等三角形的判定与性质,平行四边形的性质,菱形的判定和性质,熟记定理是解题的关键.

练习册系列答案
相关题目
16.点A(-3,-5)向左平移3个单位,再向上平移4个单位到点B,则点B的坐标为( )
| A. | (1,-8) | B. | (1,-2) | C. | (-6,-1) | D. | (0,-1) |
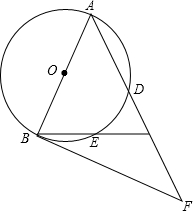 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CAB=2∠CBF.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CAB=2∠CBF.
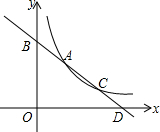 如图,一次函数y=-$\frac{\sqrt{3}}{2}$x+3$\sqrt{3}$与反比例函数y=$\frac{a}{x}$的图象交于点A(2,2$\sqrt{3}$),点C(4,b).
如图,一次函数y=-$\frac{\sqrt{3}}{2}$x+3$\sqrt{3}$与反比例函数y=$\frac{a}{x}$的图象交于点A(2,2$\sqrt{3}$),点C(4,b).