题目内容
4.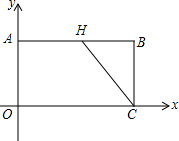 如图,在平面直角坐标系xOy中,长方形COAB的顶点A的坐标是(0,4),顶点C的坐标是(8,0),H是AB上一点,当AH=HC时,求直线CH的解析式.
如图,在平面直角坐标系xOy中,长方形COAB的顶点A的坐标是(0,4),顶点C的坐标是(8,0),H是AB上一点,当AH=HC时,求直线CH的解析式.
分析 设AH=x,则BH=8-x,在直角△BCH中,利用勾股定理即可列方程求得x的值,则H的坐标即可求得,然后利用待定系数法即可求得CH的解析式.
解答 解:∵A的坐标是(0,4),C的坐标是(8,0),
∴OA=BC=4,AB=OC=8,
设AH=x,则BH=8-x,
在直角△BCH中,CH2=BC2+BH2,即x2=42+(8-x)2,
解得:x=5,
∴AH=HC=5,
则H的坐标是(4,5),
设CH的解析式是y=kx+b,
则$\left\{\begin{array}{l}{4k+b=5}\\{8k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{5}{4}}\\{b=10}\end{array}\right.$.
则直线CH的解析式是y=-$\frac{5}{4}x$+10.
点评 本题考查了勾股定理以及待定系数法求函数的解析式,正确求得AH的长度是关键.

练习册系列答案
相关题目

 如图所示,在△ABC中,AD是∠BAC的平分线,CE是边AB上的高,若∠CDA=45°,求∠BED的度数.
如图所示,在△ABC中,AD是∠BAC的平分线,CE是边AB上的高,若∠CDA=45°,求∠BED的度数.