题目内容
12. 如图所示,在△ABC中,AD是∠BAC的平分线,CE是边AB上的高,若∠CDA=45°,求∠BED的度数.
如图所示,在△ABC中,AD是∠BAC的平分线,CE是边AB上的高,若∠CDA=45°,求∠BED的度数.
分析 作DF⊥AB于F,DG⊥EC于G,DH⊥AC交AC的延长线于H,根据角平分线的性质得到DF=DH,根据三角形的外角的性质证明∠DCH=∠DCG,证明△DCG≌△DCH,
得到DH=DG,根据角平分线的定义得到答案.
解答 解: 作DF⊥AB于F,DG⊥EC于G,DH⊥AC交AC的延长线于H,
作DF⊥AB于F,DG⊥EC于G,DH⊥AC交AC的延长线于H,
∵AD是∠BAC的平分线,DF⊥AB,DH⊥AC,
∴DF=DH,
∠DCH=45°+∠DAC,
∠DCG=90°-∠B
=90°-(∠ADC-∠BAD)
=45°+∠BAD,
∵AD是∠BAC的平分线,
∴∠DAC=∠BAD,
∴∠DCH=∠DCG,
在△DCG和△DCH中,
$\left\{\begin{array}{l}{∠DCG=∠DCH}\\{∠DGC=∠DHC}\\{CD=CD}\end{array}\right.$,
∴△DCG≌△DCH,
∴DH=DG,又DF=DH,
∴DF=DG,
∴ED平分∠BEC,又CE是边AB上的高,
∴∠BED=45°.
点评 本题考查的是三角形的角平分线、中线和高的概念和性质以及三角形全等的判定和性质,掌握角平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
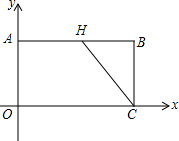 如图,在平面直角坐标系xOy中,长方形COAB的顶点A的坐标是(0,4),顶点C的坐标是(8,0),H是AB上一点,当AH=HC时,求直线CH的解析式.
如图,在平面直角坐标系xOy中,长方形COAB的顶点A的坐标是(0,4),顶点C的坐标是(8,0),H是AB上一点,当AH=HC时,求直线CH的解析式.