题目内容
15.从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).(1)上述操作能验证的等式是B(填A或B)
A、a2-2ab+b2=(a-b)2
B、a2-b2=(a+b)(a-b)
(2)应用你从(1)中选出的等式,计算:
(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)(1-$\frac{1}{{4}^{2}}$)…(1-$\frac{1}{{9}^{2}}$)(1-$\frac{1}{1{0}^{2}}$).
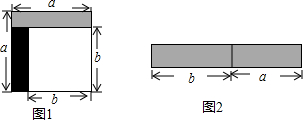
分析 (1)根据题意,将前后两个图形的面积表示出来即可.
(2)根据平方差公式即可求出答案.
解答 解:(1)图1中,边长为a的正方形的面积为:a2,
边长为b的正方形的面积为:b2,
∴图1的阴影部分为面积为:a2-b2,
图2中长方形的长为:a+b,
长方形的宽为:a-b,
∴图2长方形的面积为:(a+b)(a-b),
故选(B)
(2)原式=(1+$\frac{1}{2}$)(1-$\frac{1}{2}$)(1+$\frac{1}{3}$)(1-$\frac{1}{3}$)…(1+$\frac{1}{10}$)(1-$\frac{1}{10}$)
=$\frac{3}{2}$×$\frac{1}{2}$×$\frac{4}{3}$×$\frac{2}{3}$…$\frac{11}{10}$×$\frac{9}{10}$
=$\frac{1}{2}$×$\frac{11}{10}$
=$\frac{11}{20}$
点评 本题考查平方差公式的几何背景,解题的关键是灵活运用平方差公式,本题属于基础基础题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
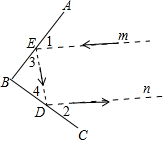 如图,平面镜AB、BC相交于点B,一束光线m射到平面镜AB、BC上,经过在E、D两点反射出去,此时有∠1=∠3,∠2=∠4
如图,平面镜AB、BC相交于点B,一束光线m射到平面镜AB、BC上,经过在E、D两点反射出去,此时有∠1=∠3,∠2=∠4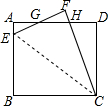 如图,在长方形ABCD中,AB=6,BC=8,E为AB上一点,将△CBE沿CE翻折至△CFE,EF,CF分别与AD交于点G、H,若EG=GH,则AE的长为1.2.
如图,在长方形ABCD中,AB=6,BC=8,E为AB上一点,将△CBE沿CE翻折至△CFE,EF,CF分别与AD交于点G、H,若EG=GH,则AE的长为1.2. 如图,四边形ABCD内接于⊙O,若∠A:∠C=5:7,则∠A=75度.
如图,四边形ABCD内接于⊙O,若∠A:∠C=5:7,则∠A=75度. 如图是城市中某区域的示意图,小聪同学从点O出发,先向西走100米,再向南走200米到达学校,如果学校的位置用(-100,-200)表示,那么(300,200)表示的地点是超市.
如图是城市中某区域的示意图,小聪同学从点O出发,先向西走100米,再向南走200米到达学校,如果学校的位置用(-100,-200)表示,那么(300,200)表示的地点是超市.