题目内容
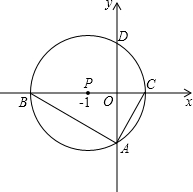 如图,以点P(-1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=2
如图,以点P(-1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=2| 3 |
(1)求B、C两点的坐标;
(2)请在图中画出线段MB、MC,并判断四边形ACMB的形状(不必证明),求出点M的坐标;
(3)动直线l从与BM重合的位置开始绕点B顺时针旋转,到与BC重合时停止,设直线l与CM交点为E,点Q为BE的中点,过点E作EG⊥BC于G,连接MQ、QG.请问在旋转过程中∠MQG的大小是否变化?若不变,求出∠MQG的度数;若变化,请说明理由.
考点:圆的综合题
专题:压轴题
分析:(1)连接PA,运用垂径定理及勾股定理即可求出圆的半径,从而可以求出B、C两点的坐标.
(2)由于圆P是中心对称图形,显然射线AP与圆P的交点就是所需画的点M,连接MB、MC即可;易证四边形ACMB是矩形;过点M作MH⊥BC,垂足为H,易证△MHP≌△AOP,从而求出MH、OH的长,进而得到点M的坐标.
(3)易证点E、M、B、G在以点Q为圆心,QB为半径的圆上,从而得到∠MQG=2∠MBG.易得∠OCA=60°,从而得到∠MBG=60°,进而得到∠MQG=120°,所以∠MQG是定值.
(2)由于圆P是中心对称图形,显然射线AP与圆P的交点就是所需画的点M,连接MB、MC即可;易证四边形ACMB是矩形;过点M作MH⊥BC,垂足为H,易证△MHP≌△AOP,从而求出MH、OH的长,进而得到点M的坐标.
(3)易证点E、M、B、G在以点Q为圆心,QB为半径的圆上,从而得到∠MQG=2∠MBG.易得∠OCA=60°,从而得到∠MBG=60°,进而得到∠MQG=120°,所以∠MQG是定值.
解答:解:(1)连接PA,如图1所示.
∵PO⊥AD,
∴AO=DO.
∵AD=2
,
∴OA=
.
∵点P坐标为(-1,0),
∴OP=1.
∴PA=
=2.
∴BP=CP=2.
∴B(-3,0),C(1,0).
(2)连接AP,延长AP交⊙P于点M,连接MB、MC.
如图2所示,线段MB、MC即为所求作.
四边形ACMB是矩形.
理由如下:
∵△MCB由△ABC绕点P旋转180°所得,
∴四边形ACMB是平行四边形.
∵BC是⊙P的直径,
∴∠CAB=90°.
∴平行四边形ACMB是矩形.
过点M作MH⊥BC,垂足为H,如图2所示.
在△MHP和△AOP中,
∵∠MHP=∠AOP,∠HPM=∠OPA,MP=AP,
∴△MHP≌△AOP.
∴MH=OA=
,PH=PO=1.
∴OH=2.
∴点M的坐标为(-2,
).
(3)在旋转过程中∠MQG的大小不变.
∵四边形ACMB是矩形,
∴∠BMC=90°.
∵EG⊥BO,
∴∠BGE=90°.
∴∠BMC=∠BGE=90°.
∵点Q是BE的中点,
∴QM=QE=QB=QG.
∴点E、M、B、G在以点Q为圆心,QB为半径的圆上,如图3所示.
∴∠MQG=2∠MBG.
∵∠COA=90°,OC=1,OA=
,
∴tan∠OCA=
=
.
∴∠OCA=60°.
∴∠MBC=∠BCA=60°.
∴∠MQG=120°.
∴在旋转过程中∠MQG的大小不变,始终等于120°.
∵PO⊥AD,

∴AO=DO.
∵AD=2
| 3 |
∴OA=
| 3 |
∵点P坐标为(-1,0),
∴OP=1.
∴PA=
| OP2+OA2 |
∴BP=CP=2.
∴B(-3,0),C(1,0).
(2)连接AP,延长AP交⊙P于点M,连接MB、MC.
如图2所示,线段MB、MC即为所求作.
四边形ACMB是矩形.
理由如下:

∵△MCB由△ABC绕点P旋转180°所得,
∴四边形ACMB是平行四边形.
∵BC是⊙P的直径,
∴∠CAB=90°.
∴平行四边形ACMB是矩形.
过点M作MH⊥BC,垂足为H,如图2所示.
在△MHP和△AOP中,
∵∠MHP=∠AOP,∠HPM=∠OPA,MP=AP,
∴△MHP≌△AOP.
∴MH=OA=
| 3 |
∴OH=2.
∴点M的坐标为(-2,
| 3 |
(3)在旋转过程中∠MQG的大小不变.

∵四边形ACMB是矩形,
∴∠BMC=90°.
∵EG⊥BO,
∴∠BGE=90°.
∴∠BMC=∠BGE=90°.
∵点Q是BE的中点,
∴QM=QE=QB=QG.
∴点E、M、B、G在以点Q为圆心,QB为半径的圆上,如图3所示.
∴∠MQG=2∠MBG.
∵∠COA=90°,OC=1,OA=
| 3 |
∴tan∠OCA=
| OA |
| OC |
| 3 |
∴∠OCA=60°.
∴∠MBC=∠BCA=60°.
∴∠MQG=120°.
∴在旋转过程中∠MQG的大小不变,始终等于120°.
点评:本题考查了垂径定理、勾股定理、全等三角形的判定与性质、矩形的判定与性质、圆周角定理、特殊角的三角函数、图形的旋转等知识,综合性比较强.证明点E、M、B、G在以点Q为圆心,QB为半径的圆上是解决第三小题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 如图,二次函数的图象与x轴交于A(-3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
如图,二次函数的图象与x轴交于A(-3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D. 下面的图象反映的过程是:红丽从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家.其中x表示时间,y表示红丽离家的距离.
下面的图象反映的过程是:红丽从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家.其中x表示时间,y表示红丽离家的距离.
 如图,在四边形ABCD中,E、F是BD上的两点,AE∥CF,AE=CF,BE=DF,求证:AD=BC.
如图,在四边形ABCD中,E、F是BD上的两点,AE∥CF,AE=CF,BE=DF,求证:AD=BC.