题目内容
两个长为2cm,宽为1cm的长方形,摆放在直线l上(如图①),CE=2cm,将长方形ABCD绕着点C顺时针旋转α角,将长方形EFGH绕着点E逆时针旋转相同的角度.

(1)当旋转到顶点D、H重合时,连接AE、CG,求证:△AED≌△GCD(如图②).
(2)当α=45°时(如图③),求证:四边形MHND为正方形.

(1)当旋转到顶点D、H重合时,连接AE、CG,求证:△AED≌△GCD(如图②).
(2)当α=45°时(如图③),求证:四边形MHND为正方形.
考点:旋转的性质,全等三角形的判定与性质,矩形的性质,正方形的判定
专题:几何综合题
分析:(1)由全等三角形的判定定理SAS证得:△AED≌△GCD(如图②);
(2)通过判定四边形MHND四个角是90°,且邻边DN=NH来判定四边形MHND是正方形.
(2)通过判定四边形MHND四个角是90°,且邻边DN=NH来判定四边形MHND是正方形.
解答:证明:(1)如图②,∵由题意知,AD=GD,ED=CD,∠ADC=∠GDE=90°,
∴∠ADC+∠CDE=∠GDE+∠CDE,即∠ADE=∠GDC,
在△AED与△GCD中,
,
∴△AED≌△GCD(SAS);
(2)如图③,∵α=45°,BC∥EH,
∴∠NCE=∠NEC=45°,CN=NE,
∴∠CNE=90°,
∴∠DNH=90°,
∵∠D=∠H=90°,
∴四边形MHND是矩形,
∵CN=NE,
∴DN=NH,
∴矩形MHND是正方形.
∴∠ADC+∠CDE=∠GDE+∠CDE,即∠ADE=∠GDC,
在△AED与△GCD中,
|
∴△AED≌△GCD(SAS);
(2)如图③,∵α=45°,BC∥EH,
∴∠NCE=∠NEC=45°,CN=NE,
∴∠CNE=90°,
∴∠DNH=90°,
∵∠D=∠H=90°,
∴四边形MHND是矩形,
∵CN=NE,
∴DN=NH,
∴矩形MHND是正方形.
点评:本题考查旋转的性质,全等三角形的判定以及正方形的判定的方法.(旋转的性质:对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等.正方形的判定的方法:两邻边相等的矩形是正方形.)

练习册系列答案
相关题目
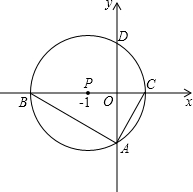 如图,以点P(-1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=2
如图,以点P(-1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=2