题目内容
 如图,有一块不规则的菜地ABCD,已知∠ABC=90°,AB=3m,BC=4m,AD=12m,CD=13m,求这块菜地的面积.
如图,有一块不规则的菜地ABCD,已知∠ABC=90°,AB=3m,BC=4m,AD=12m,CD=13m,求这块菜地的面积.考点:勾股定理,勾股定理的逆定理
专题:
分析:先根据勾股定理求出AC的长度,再根据勾股定理的逆定理判断出△ACD的形状,再利用三角形的面积公式求解即可.
解答: 解:连接AC.
解:连接AC.
∵∠ABC=90°,AB=3m,BC=4m,
∴AC=
=5
又∵AD=12m,CD=13m,
∴AC2+AD2=CD2
∴∠CAD=90°
∴菜地的面积=
(AC•AD-AB•BC)
=
(5×12-3×4)
=24(m2)
答:这块菜地的面积是24m2.
 解:连接AC.
解:连接AC.∵∠ABC=90°,AB=3m,BC=4m,
∴AC=
| AB2+BC2 |
又∵AD=12m,CD=13m,
∴AC2+AD2=CD2
∴∠CAD=90°
∴菜地的面积=
| 1 |
| 2 |
=
| 1 |
| 2 |
=24(m2)
答:这块菜地的面积是24m2.
点评:本题考查的是勾股定理的逆定理及三角形的面积,能根据勾股定理的逆定理判断出△ACD的形状是解答此题的关键.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
下列说法正确的是( )
| A、经过一点有且只有一条直线与已知直线平行 |
| B、直线外一点到这条直线的垂线段,叫做点到直线的距离 |
| C、同一平面内,不相交的两条直线是平行线 |
| D、“相等的角是对顶角”是真命题 |
某种感冒病毒的直径是0.00000012米,用科学记数法表示为( )米.
| A、1.2×10-7 |
| B、0.12×10-7 |
| C、1.2×10-6 |
| D、0.12×10-6 |

 已知∠α,利用尺规作∠AOB,使∠AOB=2∠α,请写出作法并作出图形(保留作图痕迹).
已知∠α,利用尺规作∠AOB,使∠AOB=2∠α,请写出作法并作出图形(保留作图痕迹).
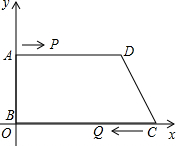 如图,直角梯形ABCD放在平面直角坐标系中,A(0,5),B(0,0),C(26,0),D(24,5)动点P,从A开始沿AD边向D以1cm/s的速度运动,动点Q从点C开始沿CB以3cm/s的速度向点B运动.P、Q同时出发,当其中一点到达顶点时,另一点也随之停止运动,设运动时间为ts,问:
如图,直角梯形ABCD放在平面直角坐标系中,A(0,5),B(0,0),C(26,0),D(24,5)动点P,从A开始沿AD边向D以1cm/s的速度运动,动点Q从点C开始沿CB以3cm/s的速度向点B运动.P、Q同时出发,当其中一点到达顶点时,另一点也随之停止运动,设运动时间为ts,问: