题目内容
在梯形ABCD中,AB∥CD,∠B=90°,AB=BC=3cm,CD=4cm.动点P从点A出发,先以2cm/s的速度沿A→B→C运动,然后以1cm/s的速度沿C→D运动,动点Q从点C出发,以0.5cm/s速度沿C→D运动,P,Q两点同时出发,当其中一个点到达终点时,运动结束.设点P运动的时间为t秒:
①当t为何值时,P、Q两点相遇?
②当t为何值时,BP=CQ?
③是否存在这样的t,使得△BPD的面积S=3cm2?
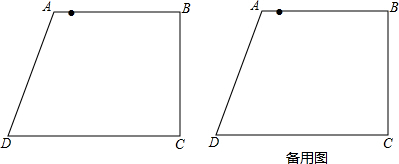
①当t为何值时,P、Q两点相遇?
②当t为何值时,BP=CQ?
③是否存在这样的t,使得△BPD的面积S=3cm2?

考点:梯形,一元一次方程的应用,三角形的面积
专题:动点型
分析:①根据已知得出方程,求出方程的解即可;
②分为两种情况,根据BP=CQ得出方程,求出方程的解即可;
③分为三种情况:根据三角形的面积得出方程,求出方程的解即可.
②分为两种情况,根据BP=CQ得出方程,求出方程的解即可;
③分为三种情况:根据三角形的面积得出方程,求出方程的解即可.
解答:解:①∵AB=BC=3cm,
∴当2t=3+3+0.5t时,P、Q两点相遇,
解得:t=4,
即当t为4s时,P、Q两点相遇;
②分为两种情况:如图1,当P在AB上时,
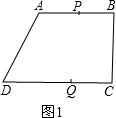
3-2t=0.5t,
解得:t=
;
如图2,当P在BC上时,
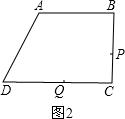
2t-3=0.5t,
解得:t=2,
即当t=
s或2s时,BP=CQ;
③存在时间t,使△BPD的面积=3cm2,
理由是:分为三种情况:如图3,当P在AB上时,
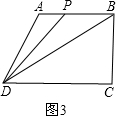
×BP×BC=3,
即
(3-2t)•3=3,
解得:t=
;
如图4,当P在BC上时,
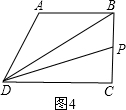
×BP×CD=3,
即
(2t-3)•4=3,
解得:t=
;
如图5,当P在DC上时,
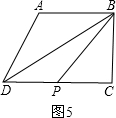
DP×BC=3,
即
•(3+3+4-2t)•3=3,
解得:t=5;
所以,存在时间t(t为
s或
s或5s),使△BPD的面积S=3cm2.
∴当2t=3+3+0.5t时,P、Q两点相遇,
解得:t=4,
即当t为4s时,P、Q两点相遇;
②分为两种情况:如图1,当P在AB上时,

3-2t=0.5t,
解得:t=
| 6 |
| 5 |
如图2,当P在BC上时,

2t-3=0.5t,
解得:t=2,
即当t=
| 6 |
| 5 |
③存在时间t,使△BPD的面积=3cm2,
理由是:分为三种情况:如图3,当P在AB上时,

| 1 |
| 2 |
即
| 1 |
| 2 |
解得:t=
| 1 |
| 2 |
如图4,当P在BC上时,

| 1 |
| 2 |
即
| 1 |
| 2 |
解得:t=
| 9 |
| 4 |
如图5,当P在DC上时,

| 1 |
| 2 |
即
| 1 |
| 2 |
解得:t=5;
所以,存在时间t(t为
| 1 |
| 2 |
| 9 |
| 4 |
点评:本题考查了直角梯形,三角形的面积的应用,用了分类讨论思想,题目是一道比较好的题目,难度适中.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
 已知∠α,利用尺规作∠AOB,使∠AOB=2∠α,请写出作法并作出图形(保留作图痕迹).
已知∠α,利用尺规作∠AOB,使∠AOB=2∠α,请写出作法并作出图形(保留作图痕迹).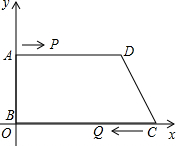 如图,直角梯形ABCD放在平面直角坐标系中,A(0,5),B(0,0),C(26,0),D(24,5)动点P,从A开始沿AD边向D以1cm/s的速度运动,动点Q从点C开始沿CB以3cm/s的速度向点B运动.P、Q同时出发,当其中一点到达顶点时,另一点也随之停止运动,设运动时间为ts,问:
如图,直角梯形ABCD放在平面直角坐标系中,A(0,5),B(0,0),C(26,0),D(24,5)动点P,从A开始沿AD边向D以1cm/s的速度运动,动点Q从点C开始沿CB以3cm/s的速度向点B运动.P、Q同时出发,当其中一点到达顶点时,另一点也随之停止运动,设运动时间为ts,问: (1)如图,矩形ONEF的对角线交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为
(1)如图,矩形ONEF的对角线交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为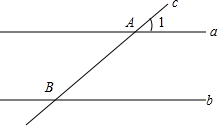 如图,直线a∥b,直线与直线a、b分别交与点A、B且∠1=45°.
如图,直线a∥b,直线与直线a、b分别交与点A、B且∠1=45°.