题目内容
2．已知x：y：z=7：5：3，且x+y=24，求x，y，z的值．分析 根据比的意义，可用a表示x，用a表示y，用a表示z，根据解方程，可得a的值，可得答案．
解答 解：由x：y：z=7：5：3，得
x=7a，y=5a，z=3a．
由x+y=24得
7a+5a=24．
解得a=2，
x=7a=14，y=5a=10，z=3a=6．
点评 本题考查了比例的性质，利用比的意义得出x=7a，y=5a，z=3a是解题关键．
练习册系列答案
同步轻松练习系列答案
相关题目
17．解方程（x+1）（x+3）=5较为合适的方法（ ）
| A． | 直接开平方法 | B． | 配方法 | C． | 公式法或配方法 | D． | 分解因式法 |
14．下列说法错误的是（ ）
| A． | 若ab＞0，则$\frac{b}{a}＞0$ | B． | 若$\frac{b}{a}＜0$，则ab＜0 | ||
| C． | 若ac＜0，$\frac{ab}{c}＞0$，则b＜0 | D． | 若ac＞0，bc＞0，则abc＞0 |
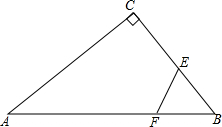如图，Rt△ABC中，∠ACB=90°，AB=8cm，BC=6cm，F点以2cm/秒的速度在线段AB上由A向B匀速运动，E点同时以1cm/秒的速度在线段BC上由B向C匀速运动，设运动时间为t秒（0＜t＜4）．