题目内容
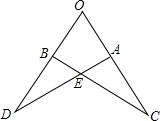 如图,已知:∠C=∠D,OD=OC.求证:DE=CE.
如图,已知:∠C=∠D,OD=OC.求证:DE=CE.考点:全等三角形的判定与性质
专题:证明题
分析:易证△OBC≌△OAD,可得OA=OB,即可求得AC=BD,即可证明△ACE≌△BDE,根据全等三角形对应边相等的性质即可解题.
解答:证明:在△OBC和△OAD中,
,
∴△OBC≌△OAD(ASA),
∴OA=OB,
∵OD=OC,
∴OD-OB=OC-OA,即AC=BD,
在△ACE和△BDE中,
,
∴△ACE≌△BDE(AAS),
∴DE=CE.
|
∴△OBC≌△OAD(ASA),
∴OA=OB,
∵OD=OC,
∴OD-OB=OC-OA,即AC=BD,
在△ACE和△BDE中,
|
∴△ACE≌△BDE(AAS),
∴DE=CE.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△OBC≌△OAD和△ACE≌△BDE是解题的关键.

练习册系列答案
相关题目
若抛物线y=x2-2x+c与y轴的交点为(0,-3),则该抛物线与x轴的交点是( )
| A、(-1,0)和(0,3) |
| B、(0,-1)和(3,0) |
| C、(-1,0)和(3,0) |
| D、(0,-1)和(0,3) |
已知⊙O的半径为3,线段OP的长度为2,则点P与⊙O的位置关系是( )
| A、点P在⊙O内 |
| B、点P在⊙O上 |
| C、点P在⊙O外 |
| D、无法确定 |
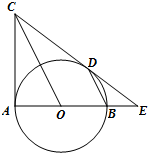 如图,已知AB为⊙O的直径,AC为⊙O的切线,连结CO.BD∥OC交⊙O于D,延长AB、CD交于点E.
如图,已知AB为⊙O的直径,AC为⊙O的切线,连结CO.BD∥OC交⊙O于D,延长AB、CD交于点E.