Question

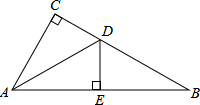
如图，在△ABC中，∠C=90°，AD平分∠BAC，若AB=10，BD=4，则tan

A

2

=

 

．

Answer 1

考点：角平分线的性质,勾股定理,锐角三角函数的定义

专题：

分析：过点D作DE⊥AB，由角平分线的性质可知DE=CD，根据相似求出

CD

AC

=

DE

AC

=

BD

AB

=

2

5

，即可求出答案．

解答：解：
过D做DE⊥AB于E，
∵在△ABC中，∠C=90°，AD平分∠BAC，
∴DE=DC，
∵∠DEB=∠C=90°，∠B=∠B，
∴△BED∽△BCA，
∴

DE

AC

=

BD

AB

=

4

10

=

2

5

，
∴

CD

AC

=

2

5

，
∴tan

A

2

=tan∠CAD=

CD

AC

=

2

5

，
故答案为：

2

5

．

点评：本题考查了角平分线的性质，相似三角形的性质和判定的应用，解此题的关键是求出DE=DC和求出

DE

AC

的值．