题目内容
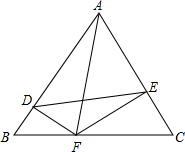 △ABC为等边三角形,边长为a,DF⊥AB,EF⊥AC,
△ABC为等边三角形,边长为a,DF⊥AB,EF⊥AC,(1)求证:△BDF∽△CEF;
(2)若a=4,设BF=m,四边形ADFE面积为S,求出S与m之间的函数关系,并探究当m为何值时S取最大值;
(3)已知A、D、F、E四点共圆,已知tan∠EDF=
| ||
| 2 |
考点:相似形综合题,二次函数的最值,等边三角形的性质,圆周角定理,解直角三角形
专题:综合题,探究型
分析:(1)只需找到两组对应角相等即可.
(2)四边形ADFE面积S可以看成△ADF与△AEF的面积之和,借助三角函数用m表示出AD、DF、AE、EF的长,进而可以用含m的代数式表示S,然后通过配方,转化为二次函数的最值问题,就可以解决问题.
(3)易知AF就是圆的直径,利用圆周角定理将∠EDF转化为∠EAF.在△AFC中,知道tan∠EAF、∠C、AC,通过解直角三角形就可求出AF长.
(2)四边形ADFE面积S可以看成△ADF与△AEF的面积之和,借助三角函数用m表示出AD、DF、AE、EF的长,进而可以用含m的代数式表示S,然后通过配方,转化为二次函数的最值问题,就可以解决问题.
(3)易知AF就是圆的直径,利用圆周角定理将∠EDF转化为∠EAF.在△AFC中,知道tan∠EAF、∠C、AC,通过解直角三角形就可求出AF长.
解答: 解:(1)∵DF⊥AB,EF⊥AC,
解:(1)∵DF⊥AB,EF⊥AC,
∴∠BDF=∠CEF=90°.
∵△ABC为等边三角形,
∴∠B=∠C=60°.
∵∠BDF=∠CEF,∠B=∠C,
∴△BDF∽△CEF.
(2)∵∠BDF=90°,∠B=60°,
∴sin60°=
=
,cos60°=
=
.
∵BF=m,
∴DF=
m,BD=
.
∵AB=4,
∴AD=4-
.
∴S△ADF=
AD•DF
=
×(4-
)×
m
=-
m2+
m.
同理:S△AEF=
AE•EF
=
×(4-
)×
(4-m)
=-
m2+2
.
∴S=S△ADF+S△AEF
=-
m2+
m+2
=-
(m2-4m-8)
=-
(m-2)2+3
.其中0<m<4.
∵-
<0,0<2<4,
∴当m=2时,S取最大值,最大值为3
.
∴S与m之间的函数关系为:
S═-
(m-2)2+3
(其中0<m<4).
当m=2时,S取到最大值,最大值为3
.
(3)如图2,
∵A、D、F、E四点共圆,
∴∠EDF=∠EAF.
∵∠ADF=∠AEF=90°,
∴AF是此圆的直径.
∵tan∠EDF=
,
∴tan∠EAF=
.
∴
=
.
∵∠C=60°,
∴
=tan60°=
.
设EC=x,则EF=
x,EA=2x.
∵AC=a,
∴2x+x=a.
∴x=
.
∴EF=
a,AE=
a.
∵∠AEF=90°,
∴AF=
=
a.
∴此圆直径长为
a.
 解:(1)∵DF⊥AB,EF⊥AC,
解:(1)∵DF⊥AB,EF⊥AC,∴∠BDF=∠CEF=90°.
∵△ABC为等边三角形,
∴∠B=∠C=60°.
∵∠BDF=∠CEF,∠B=∠C,
∴△BDF∽△CEF.
(2)∵∠BDF=90°,∠B=60°,
∴sin60°=
| DF |
| BF |
| ||
| 2 |
| BD |
| BF |
| 1 |
| 2 |
∵BF=m,
∴DF=
| ||
| 2 |
| m |
| 2 |
∵AB=4,
∴AD=4-
| m |
| 2 |
∴S△ADF=
| 1 |
| 2 |
=
| 1 |
| 2 |
| m |
| 2 |
| ||
| 2 |
=-
| ||
| 8 |
| 3 |
同理:S△AEF=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 4-m |
| 2 |
| ||
| 2 |
=-
| ||
| 8 |
| 3 |
∴S=S△ADF+S△AEF
=-
| ||
| 4 |
| 3 |
| 3 |
=-
| ||
| 4 |
=-
| ||
| 4 |
| 3 |
∵-
| ||
| 4 |
∴当m=2时,S取最大值,最大值为3
| 3 |
∴S与m之间的函数关系为:
S═-
| ||
| 4 |
| 3 |
当m=2时,S取到最大值,最大值为3
| 3 |
(3)如图2,

∵A、D、F、E四点共圆,
∴∠EDF=∠EAF.
∵∠ADF=∠AEF=90°,
∴AF是此圆的直径.
∵tan∠EDF=
| ||
| 2 |
∴tan∠EAF=
| ||
| 2 |
∴
| EF |
| EA |
| ||
| 2 |
∵∠C=60°,
∴
| EF |
| EC |
| 3 |
设EC=x,则EF=
| 3 |
∵AC=a,
∴2x+x=a.
∴x=
| a |
| 3 |
∴EF=
| ||
| 3 |
| 2 |
| 3 |
∵∠AEF=90°,
∴AF=
| AE2+EF2 |
| ||
| 3 |
∴此圆直径长为
| ||
| 3 |
点评:本题考查了相似三角形的判定、二次函数的最值、三角函数、解直角三角形、圆周角定理、等边三角形的性质等知识,综合性强.利用圆周角定理将条件中的圆周角转化到合适的位置是解决最后一小题的关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
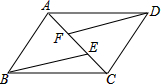 如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.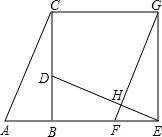 如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.
如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.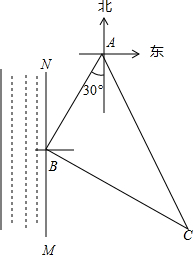 如图,小明的家位于一条南北走向的河流MN的东侧A处,某一天小明从家出发沿南偏西30°方向走60m到达河边B处取水,然后沿另一方向走80m到达菜地C处浇水,最后沿第三方向走100m回到家A处.问小明在河边B处取水后是沿哪个方向行走的?并说明理由.
如图,小明的家位于一条南北走向的河流MN的东侧A处,某一天小明从家出发沿南偏西30°方向走60m到达河边B处取水,然后沿另一方向走80m到达菜地C处浇水,最后沿第三方向走100m回到家A处.问小明在河边B处取水后是沿哪个方向行走的?并说明理由.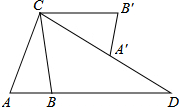 如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB、CA′相交于点D,则线段BD的长为
如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB、CA′相交于点D,则线段BD的长为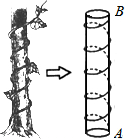 我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是
我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是