题目内容
4.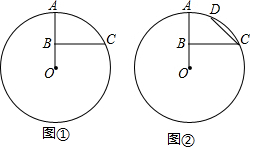 已知,点B是半径OA的中点,过点B作BC⊥OA交⊙O于点C.
已知,点B是半径OA的中点,过点B作BC⊥OA交⊙O于点C.(1)如图①,若BC=$\sqrt{3}$,求⊙O的直径;
(2)如图②,点D是$\widehat{AC}$上一点,求∠ADC的大小.
分析 (1)连接OC,根据勾股定理得出方程,求出方程的解即可;
(2)在⊙O上取一点E,连接AC,CE,连接OC,解直角三角形求出∠AOC,根据圆周角定理求出∠E,根据圆内接四边形的性质求出即可.
解答 解:(1)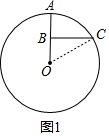
连接OC,
设OA=OC=R,则OB=AB=$\frac{1}{2}$R,
∵BC⊥OA,
∴∠CBO=90°,
由勾股定理得:OC2=BC2+OB2,
即R2=($\sqrt{3}$)2+($\frac{1}{2}$R)2,
解得:R=2,
即⊙O的直径是4;
(2)在⊙O上取一点E,连接AC,CE,连接OC,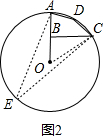
由(1)可知:sin∠BOC=$\frac{BC}{OC}$=$\frac{\sqrt{3}}{2}$,
∴∠BOC=60°,
∴∠E=$\frac{1}{2}$∠AOC=30°,
∵A、E、C、D四点共圆,
∴∠ADC+∠E=180°,
∴∠ADC=150°.
点评 本题考查了圆周角定理,勾股定理,圆内接四边形等知识点,能正确做出辅助线是解此题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:AF=2CD.
如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:AF=2CD.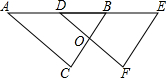 如图,△DEF是由△ABC经过平移得到的,若∠C=80°,∠A=30°,则∠E=70°.
如图,△DEF是由△ABC经过平移得到的,若∠C=80°,∠A=30°,则∠E=70°.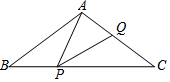 如图,在△ABC中,己知AB=AC=5 cm,BC=8 cm,点P在边BC上沿B到C的方向以每秒1 cm的速度运动(不与点B,C重合),点Q在AC上,且满足∠APQ=∠B,设点P运动时间为t秒,当△APQ是等腰三角形时,t=3秒或$\frac{39}{8}$秒.
如图,在△ABC中,己知AB=AC=5 cm,BC=8 cm,点P在边BC上沿B到C的方向以每秒1 cm的速度运动(不与点B,C重合),点Q在AC上,且满足∠APQ=∠B,设点P运动时间为t秒,当△APQ是等腰三角形时,t=3秒或$\frac{39}{8}$秒.