题目内容
方程x2-
x=k,在(-1,1)上有实根,求k的范围.
| 3 |
| 2 |
考点:二次函数的性质
专题:
分析:先由二次函数的性质得出y=x2-
x-k的对称轴为直线x=
,那么要使方程x2-
x=k在(-1,1)上有实根,则函数y=x2-
x-k有:
,依此列出不等式组
,求解即可.
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
|
|
解答:解:∵x2-
x=k,
∴x2-
x-k=0.
∵函数y=x2-
x-k的对称轴为直线x=
,
要使方程x2-
x=k在(-1,1)上有实根,
则函数y=x2-
x-k有:
,
即
,
解得-
≤k≤
.
| 3 |
| 2 |
∴x2-
| 3 |
| 2 |
∵函数y=x2-
| 3 |
| 2 |
| 3 |
| 4 |
要使方程x2-
| 3 |
| 2 |
则函数y=x2-
| 3 |
| 2 |
|
即
|
解得-
| 9 |
| 16 |
| 5 |
| 2 |
点评:本题考查了二次函数的性质,一元一次不等式组的解法,难度适中.由题意得出
是解题的关键.
|

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
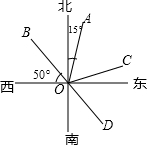 如图,OA的方向是北偏东15°,OB的方向是西偏北50°.
如图,OA的方向是北偏东15°,OB的方向是西偏北50°.