题目内容
关于x的方程x2+3mx+2m2=0(其中m≠0).
(1)请你说明无论m取何值,方程总有两个不相等的实数根;
(2)请你取一个m的值代入代数式x2+3mx+2m2中,并求出这是当x取何值时,代数式的值最小?并求出这时代数式的最小值.
(1)请你说明无论m取何值,方程总有两个不相等的实数根;
(2)请你取一个m的值代入代数式x2+3mx+2m2中,并求出这是当x取何值时,代数式的值最小?并求出这时代数式的最小值.
考点:根的判别式
专题:
分析:(1)先计算方程根的判别式△的值,得到△=(3m)2-4×2m2=m2,由于m≠0,则有△>0,然后根据△的意义即可得到结论;
(2)把这个代数式写成完全平方的形式,再根据非负数的性质求解即可.
(2)把这个代数式写成完全平方的形式,再根据非负数的性质求解即可.
解答:证明:(1)△=(3m)2-4×2m2
=m2,
∵m≠0,
∴m2>0,
∴△>0,
∴无论m取何值,此方程都有两个不相等的实数根;
(2)∵x2+3mx+2m2=(x+
m)2-
m2,
∴当x=-
m时,代数式的值最小,这时代数式的最小值是-
m2.
当m=0时,x=0,即当x=0时,代数式的值最小,这时代数式的最小值0.
=m2,
∵m≠0,
∴m2>0,
∴△>0,
∴无论m取何值,此方程都有两个不相等的实数根;
(2)∵x2+3mx+2m2=(x+
| 3 |
| 2 |
| 1 |
| 4 |
∴当x=-
| 3 |
| 2 |
| 1 |
| 4 |
当m=0时,x=0,即当x=0时,代数式的值最小,这时代数式的最小值0.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac的关系:
①当△>0时,方程有两个不相等的两个实数根;
②当△=0时,方程有两个相等的两个实数根;
③当△<0时,方程无实数根.
同时考查了配方法的应用.
①当△>0时,方程有两个不相等的两个实数根;
②当△=0时,方程有两个相等的两个实数根;
③当△<0时,方程无实数根.
同时考查了配方法的应用.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
 如图,△ABC的两条高BD、CE相交于点H,请问点A、E、H、D在同一个圆上吗?请说明理由.
如图,△ABC的两条高BD、CE相交于点H,请问点A、E、H、D在同一个圆上吗?请说明理由. 已知如图,在△ABC中,BD=CE,DF=EF,求证:AB=AC.
已知如图,在△ABC中,BD=CE,DF=EF,求证:AB=AC.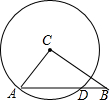 如图,在⊙C中,CA⊥CB,且CA=3,CB=4,求AD的长.
如图,在⊙C中,CA⊥CB,且CA=3,CB=4,求AD的长. 如图,已知在等边△ABC中,点D是边BC的中点,BF⊥AC于F点,连接DF并延长至E点,使得EF=DF,试判断△ACE的形状,并说明理由.
如图,已知在等边△ABC中,点D是边BC的中点,BF⊥AC于F点,连接DF并延长至E点,使得EF=DF,试判断△ACE的形状,并说明理由.