题目内容
7.已知代数式(2x2+ax-y+6)-(2bx2-3x+5y-1).(1)当a=-3,b=1时,此代数式的值与字母x的取值无关;
(2)在(1)的条件下,求多项式3(a2-2ab-b2)-(3a2+ab+b2)的值;
(3)在(1)的条件下,求(b+a2)+(2b+$\frac{1}{1×2}$•a2)+(3b+$\frac{1}{2×3}$•a2)+…+(9b+$\frac{1}{8×9}$•a2)的值.
分析 (1)先去括号,合并同类项,根据题意求出a、b即可;
(2)先去括号,合并同类项,再代入求出即可;
(3)先用适当的方法变形,再合并同类项,最后代入求出即可.
解答 解:(1)(2x2+ax-y+6)-(2bx2-3x+5y-1)
=2x2+ax-y+6-2bx2+3x-5y+1
=(2-2b)x2+(a+3)x-6y+7,
当2-2b=0,a+3=0时,此代数式的值与字母x的取值无关,
即b=1,a=-3,
故答案为:-3,1;
(2)当a=-3,b=1时,
3(a2-2ab-b2)-(3a2+ab+b2)
=3a2-6ab-3b2-3a2-ab-b2
=-7ab-4b2
=-7×(-3)×1-4×12
=17;
(3)(b+a2)+(2b+$\frac{1}{1×2}$•a2)+(3b+$\frac{1}{2×3}$•a2)+…+(9b+$\frac{1}{8×9}$•a2)
=b+a2+2b+$\frac{1}{1×2}$•a2+3b+$\frac{1}{2×3}$•a2+…+9b+$\frac{1}{8×9}$•a2
=45b+a2+a2-$\frac{1}{2}$a2+$\frac{1}{2}$a2-$\frac{1}{3}$a2+…+$\frac{1}{8}$a2-$\frac{1}{9}$a2
=45b+$\frac{17}{9}$a2
=45×1+$\frac{17}{9}$×(-3)2
=62.
点评 本题考查了多项式乘以多项式法则,整式的混合运算和求值的应用,能正确根据整式的运算法则进行化简是解此题的关键.

练习册系列答案
相关题目
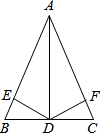 如图,在△ABC中,AB=AC,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,若DE=3,则DF=3.
如图,在△ABC中,AB=AC,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,若DE=3,则DF=3.