题目内容
7. 如图,⊙O的直径AB垂直弦CD于点E,AB=8,∠A=22.5°,求CD的长.
如图,⊙O的直径AB垂直弦CD于点E,AB=8,∠A=22.5°,求CD的长.
分析 根据圆周角定理得出∠COE的度数,在Rt△ACE中,由三角函数的定义得出CE,再由垂径定理得出CD即可.
解答 解:∵AB=8,
∴OC=OA=4,
∵∠A=22.5°,
∴∠COE=2∠A=45°,
∵直径AB垂直弦CD于E,
∴$CE=OC•sin45°=2\sqrt{2}$,
∴$CD=4\sqrt{2}$.
点评 本题考查了垂径定理,还考查了圆周角定理、三角函数的定义,掌握三角函数的定义是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15. 如图,点A、B、C、D为圆O的四等分点,动点P从圆心O出发,沿线段OC-弧CD-线段DO的路线作匀速运动.设运动时间为t秒,∠APB的度数为y度,则下列图象中表示y与t的函数关系最恰当的是( )
如图,点A、B、C、D为圆O的四等分点,动点P从圆心O出发,沿线段OC-弧CD-线段DO的路线作匀速运动.设运动时间为t秒,∠APB的度数为y度,则下列图象中表示y与t的函数关系最恰当的是( )
 如图,点A、B、C、D为圆O的四等分点,动点P从圆心O出发,沿线段OC-弧CD-线段DO的路线作匀速运动.设运动时间为t秒,∠APB的度数为y度,则下列图象中表示y与t的函数关系最恰当的是( )
如图,点A、B、C、D为圆O的四等分点,动点P从圆心O出发,沿线段OC-弧CD-线段DO的路线作匀速运动.设运动时间为t秒,∠APB的度数为y度,则下列图象中表示y与t的函数关系最恰当的是( )| A. | 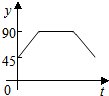 | B. | 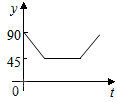 | C. | 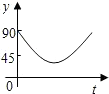 | D. | 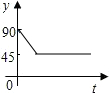 |
2.下列说法中,正确的是( )
| A. | 不可能事件发生的概率是0 | |
| B. | 打开电视机正在播放动画片,是必然事件 | |
| C. | 随机事件发生的概率是 $\frac{1}{2}$ | |
| D. | 对“梦想的声音”节目收视率的调查,宜采用普查 |
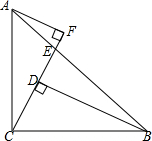 已知:如图,Rt△ABC中,AC=BC,∠ACB=90°,CF交AB于点E,BD⊥CF于点D,AF⊥CF.
已知:如图,Rt△ABC中,AC=BC,∠ACB=90°,CF交AB于点E,BD⊥CF于点D,AF⊥CF.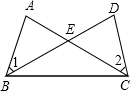 已知:如图,AB=DC,∠1=∠2.求证:∠EBC=∠ECB.
已知:如图,AB=DC,∠1=∠2.求证:∠EBC=∠ECB. 如图,点B、E、C、F在同一直线上,∠A=∠D,AB∥DE,AB=DE.求证:BE=CF.
如图,点B、E、C、F在同一直线上,∠A=∠D,AB∥DE,AB=DE.求证:BE=CF.