题目内容
12. 如图,△EDC是由△EAB绕点E顺时针旋转40°后得到的图形,则∠BFD的度数是40°.
如图,△EDC是由△EAB绕点E顺时针旋转40°后得到的图形,则∠BFD的度数是40°.
分析 连接BD,可将∠BFD放到△BDF中根据内角和定理来求,由旋转性质知∠BED=40°、ED=EB可得∠EBD=∠EDB=∠EDC+∠FDB=70°,而∠EDC=∠EBA,得∠EBA+∠FDB+∠EBD即可.
解答 解:如图,连接BD,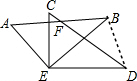
由旋转性质可得,∠BED=40°,ED=EB,∠EDC=∠EBA,
∴∠EBD=∠EDB=∠EDC+∠FDB=$\frac{180°-40°}{2}$=70°,
∵∠EDC=∠EBA,
∴∠EBA+∠FDB=∠EBD=70°,
∴在△BDF中,∠BFD=180°-(∠EBA+∠FDB+∠EBD)=40°,
故答案为:40.
点评 本题主要考查旋转的性质,熟练掌握并灵活旋转的性质是解决此题的基本要求,将∠BFD放到△BDF中根据内角和定理去求是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.下列命题中,是真命题的是( )
| A. | 三个点确定一个圆 | |
| B. | 同弧所对的圆周角与圆心角相等 | |
| C. | 直径是圆中最长的弦 | |
| D. | 圆是轴对称图形,不是中心对称图形 |

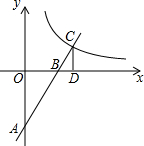 如图,直线y=2x-4的图象与x、y轴交于B、A两点,与y=$\frac{k}{x}$的图象交于点C,CD⊥x轴于点D,如果△CDB的面积:△AOB的面积=1:4,则k的值为6.
如图,直线y=2x-4的图象与x、y轴交于B、A两点,与y=$\frac{k}{x}$的图象交于点C,CD⊥x轴于点D,如果△CDB的面积:△AOB的面积=1:4,则k的值为6.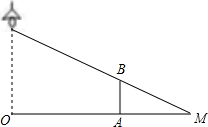 如图,路灯垂直照射在地面的位置为点O,小华(用线段AB表示)站在离路灯不远的A处,在路灯的照射(中心投影)下,可形成小华的影子是线段AM.
如图,路灯垂直照射在地面的位置为点O,小华(用线段AB表示)站在离路灯不远的A处,在路灯的照射(中心投影)下,可形成小华的影子是线段AM.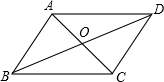 如图,在平行四边形ABCD中,连接AC,BD并相交于点O,你发现0A与OC,OB与0D有什么数量关系?并证明你发现的结论.
如图,在平行四边形ABCD中,连接AC,BD并相交于点O,你发现0A与OC,OB与0D有什么数量关系?并证明你发现的结论.