题目内容
19.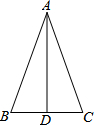 已知:如图所示,在锐角△ABC中,AD平分∠BAC,且BD=CD.
已知:如图所示,在锐角△ABC中,AD平分∠BAC,且BD=CD.求证:△ABC是等腰三角形.
分析 首先延长AD至E,使AD=DE,连接BE,根据三角形全等的判定方法,可得:△ADC≌△EBD;然后根据全等三角形的对应边相等,可得:∠CAD=∠BED,据此推得AB=BE=AC,判断出△ABC是等腰三角形即可.
解答 证明:如图,延长AD至E,使AD=DE,连接BE,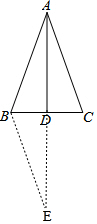 ,
,
在△ACD和△EBD中,
$\left\{\begin{array}{l}{AD=ED}\\{∠ADC=∠EDB}\\{CD=BD}\end{array}\right.$,
∴△ACD≌△EBD,
∴BE=AC,∠DAC=∠DEB,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠BAD=∠BED,
∴AB=BE,
∴AB=AC,
∴△ABC是等腰三角形.
点评 此题主要考查了等腰三角形的判定,以及三角形全等的判定方法和应用,要熟练掌握.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
8.下列各组数中,不能作为直角三角形三边长的是( )
| A. | 0.3,0.4,0.5 | B. | 8,9,10 | C. | 1,$\sqrt{2}$,$\sqrt{3}$ | D. | 11,60,61 |
9. 如图,在△ABC中,D是BC延长线上一点,∠B=50°,∠ACD=120°,则∠A=( )
如图,在△ABC中,D是BC延长线上一点,∠B=50°,∠ACD=120°,则∠A=( )
 如图,在△ABC中,D是BC延长线上一点,∠B=50°,∠ACD=120°,则∠A=( )
如图,在△ABC中,D是BC延长线上一点,∠B=50°,∠ACD=120°,则∠A=( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
14.某校计划购进A、B两种花卉,两次购进的花卉的数量与每次总费用如表所示:
(1)你从表格中获取了什么信息?请用自己的简练言,写出一条.这条信息为:购买A种花卉10株和B种花卉25株共花费225元
(2)求A、B两种花卉每株的价格分别是多少元?
| 花卉数量(株) | 总费用(元) | ||
| A | B | ||
| 第1次购买 | 10 | 25 | 225 |
| 第2次购买 | 20 | 15 | 275 |
(2)求A、B两种花卉每株的价格分别是多少元?
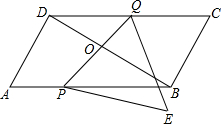 如图,在?ABCD中,O是对角线BD的中点,AD⊥BD,AB=4cm,∠BAD=60°,动点P从点A出发,以2cm/s的速度沿折线AB-BC向终点C运动,连结PO并延长交折线CD-DA于点Q,将线段PQ绕着点P顺时针旋转60°得到线段PE,连结QE,设点P的运动时间为t(s)
如图,在?ABCD中,O是对角线BD的中点,AD⊥BD,AB=4cm,∠BAD=60°,动点P从点A出发,以2cm/s的速度沿折线AB-BC向终点C运动,连结PO并延长交折线CD-DA于点Q,将线段PQ绕着点P顺时针旋转60°得到线段PE,连结QE,设点P的运动时间为t(s) 已知在平面直角坐标系xOy中,点A(0,2),点B(1,0),现将线段BA绕点B按顺时针方向旋转90°得到线段BD,点C为线段AB的中点,连接CD.
已知在平面直角坐标系xOy中,点A(0,2),点B(1,0),现将线段BA绕点B按顺时针方向旋转90°得到线段BD,点C为线段AB的中点,连接CD.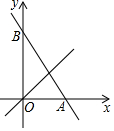 如图,一次函数y=-$\sqrt{3}$x+$\sqrt{3}$的图象与x轴、y轴交于A、B两点,P为一次函数y=x的图象上一点,以P为圆心能够画出圆与直线AB和y轴同时相切,则∠BPO=30°或120°.
如图,一次函数y=-$\sqrt{3}$x+$\sqrt{3}$的图象与x轴、y轴交于A、B两点,P为一次函数y=x的图象上一点,以P为圆心能够画出圆与直线AB和y轴同时相切,则∠BPO=30°或120°.