题目内容
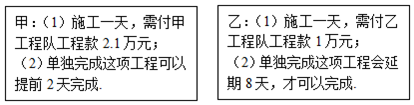
4.莆田中山中学荔兴楼需要在规定时间内改造完成,以备迎接新学期的开学.在工程招标时,接到甲、乙两个工程队的投标书如图:(部分信息)甲:(1)施工一天,需付甲工程队工程款2.1万元;
(2)单独完成这项工程可以提前2天完成.
乙:(1)施工一天,需付乙工程队工程款1万元;
(2)单独完成这项工程会延期8天,才可以完成.
学校后勤处提出两个方案:①由甲工程队单独施工;②由乙工程队单独施工;
校团委学生代表小组根据甲、乙两队的投标书测算以及工期安排,提出了新的方案③:若甲、乙两队合做4天,余下的工程由乙队单独做也正好如期完成.
试问:(1)学校规定的期限是多少天?
(2)在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.
分析 (1)设该工程的规定时间为x天,等量关系为:甲乙合作4天的工作总量+乙做(规定天数-4)天的工作量=1,依此列出方程求解即可;
(2)根据已知算出各种方案的价钱之后,再根据题意进行选择.
解答 解:(1)设该工程的规定时间为x天,则甲队需(x-2)天完成,乙队需(x+8)天完成.
由题意,可得:4($\frac{1}{x-2}$+$\frac{1}{x+8}$)+$\frac{x-4}{x+8}$=1,
解得x=12.
经检验,x=12是原方程的解.
答:学校规定的期限是12天;
(2)答:选择方案③.理由如下:
由于不耽误工期,故方案②舍去.只能选择方案①与方案③.
方案①:由甲队单独施工,10天完成.其费用M1=10×2.1=21(万元),
方案③:甲乙合作4天,再由乙队施工8天.其费用M2=4×2.1+12×1=20.4(万元),
∵M1>M2,
∴选择方案③进行施工.
点评 此题主要考查了分式方程的应用,找到合适的等量关系是解决问题的关键.在既有工程任务,又有工程费用的情况下.先考虑完成工程任务,再考虑工程费用.

练习册系列答案
相关题目
13.若分式 $\frac{x-2}{|x|-1}$的值为0,则x的取值是( )
| A. | x≠2 | B. | x≠-1 | C. | x=2 | D. | x≠±1 |
14.下列函数中,满足y的值随x的增大而增大的是( )
| A. | y=-2x | B. | y=x-3 | C. | y=$\frac{1}{x}$ | D. | y=x2 |
13.在平面直角坐标系中,已知三点O(0,0),A(1,-2),B(3,1),若以A、B、C、O为顶点的四边形是平行四边形,则C点不可能在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14. 如果边长相等的正五边形和正方形的一边重合,那么∠1的度数是多少( )
如果边长相等的正五边形和正方形的一边重合,那么∠1的度数是多少( )
 如果边长相等的正五边形和正方形的一边重合,那么∠1的度数是多少( )
如果边长相等的正五边形和正方形的一边重合,那么∠1的度数是多少( )| A. | 30° | B. | 15° | C. | 18° | D. | 20° |
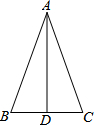 已知:如图所示,在锐角△ABC中,AD平分∠BAC,且BD=CD.
已知:如图所示,在锐角△ABC中,AD平分∠BAC,且BD=CD.