题目内容
10.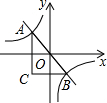 如图,反比例函数y=-$\frac{4}{x}$的图象与直线y=kx(k<0)的交点为A,B,过点A作y轴的平行线与过点B作x轴的平行线相交于点C,则△ABC的面积为( )
如图,反比例函数y=-$\frac{4}{x}$的图象与直线y=kx(k<0)的交点为A,B,过点A作y轴的平行线与过点B作x轴的平行线相交于点C,则△ABC的面积为( )| A. | 8 | B. | 6 | C. | 4 | D. | 2 |
分析 双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,根据反比例函数的中心对称特点可知△ABC的是面积2|k|.
解答 解:由于点A、B在反比例函数图象上关于原点对称,
则△ABC的面积=2|k|=2×4=8.
故选:A.
点评 主要考查了反比例函数y=$\frac{k}{x}$中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点;图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=$\frac{1}{2}$|k|.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
20. 如图所示,已知AB∥CD,直线EF交AB于点E,交CD于点F,且EG平分∠FEB,∠1=50°,则∠2等于( )
如图所示,已知AB∥CD,直线EF交AB于点E,交CD于点F,且EG平分∠FEB,∠1=50°,则∠2等于( )
 如图所示,已知AB∥CD,直线EF交AB于点E,交CD于点F,且EG平分∠FEB,∠1=50°,则∠2等于( )
如图所示,已知AB∥CD,直线EF交AB于点E,交CD于点F,且EG平分∠FEB,∠1=50°,则∠2等于( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
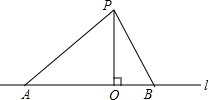 作图并回答:过点P作直线l的垂线PO,垂足为O,连接PA、PB;比较线段PO、PA、PB的长短,并按小到大的顺序排列为PO<PB<PA.
作图并回答:过点P作直线l的垂线PO,垂足为O,连接PA、PB;比较线段PO、PA、PB的长短,并按小到大的顺序排列为PO<PB<PA. 如图,已知直线l和A,B两点,求作经过A,B两点的圆,使圆心在直线l上.
如图,已知直线l和A,B两点,求作经过A,B两点的圆,使圆心在直线l上. 一辆汽车和一辆摩托车同时分别从A,B两地去同一城市,它们离A地的路程随时间变化的图象如图所示.当汽车到达目的地时,摩托车距目的地20千米.
一辆汽车和一辆摩托车同时分别从A,B两地去同一城市,它们离A地的路程随时间变化的图象如图所示.当汽车到达目的地时,摩托车距目的地20千米. 如图,B,C分别在△ADE的边AD,AE上,且AC=6,AB=5,EC=4,DB=7,则BC:DE=$\frac{1}{2}$.
如图,B,C分别在△ADE的边AD,AE上,且AC=6,AB=5,EC=4,DB=7,则BC:DE=$\frac{1}{2}$.