题目内容
10.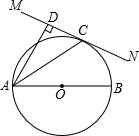 如图,己知AB为⊙O上直径,过C作直线MN,AD⊥MN于D,AC平分∠BAD,求证:MN与⊙O相切.
如图,己知AB为⊙O上直径,过C作直线MN,AD⊥MN于D,AC平分∠BAD,求证:MN与⊙O相切.
分析 连接OC,由OA=OC可以得到∠OAC=∠OCA,然后利用角平分线的性质可以证明∠DAC=∠OCA,接着利用平行线的判定即可得到OC∥AD,然后就得到OC⊥CD,由此即可证明直线MN与⊙O相切于C点.
解答  证明:连接OC,
证明:连接OC,
∵OA=OC,
∴∠OAC=∠OCA,
∵AC平分∠DAB,
∴∠DAC=∠OAC,
∴∠DAC=∠OCA,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥MN.
又∵OC是⊙O的半径,
∴直线MN与⊙O相切于点C.
点评 本题考查了切线的判定,角平分线的性质,平行线的判定和性质,等腰三角形的性质,熟练掌握性质和定理是解题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
1.数轴上与表示2的点距离等于3个单位长度的点表示的数是( )
| A. | 0或5 | B. | -1或5 | C. | -1或-5 | D. | -2或5 |
5.如图,是一个简单的数值运算程序.则输入x的值为( )

| A. | 3或-3 | B. | 4或-2 | C. | 1或3 | D. | 27 |
 如图,AB为半圆O的直径,点C是OA的中点,CD⊥OA交半圆O于点D,点E是$\widehat{BD}$的中点,过点D作DP∥AE交BA的延长线于点P.求证:
如图,AB为半圆O的直径,点C是OA的中点,CD⊥OA交半圆O于点D,点E是$\widehat{BD}$的中点,过点D作DP∥AE交BA的延长线于点P.求证: 如图,已知点C是线段AB上任意一点,M、N分别是AC、BC的中点.
如图,已知点C是线段AB上任意一点,M、N分别是AC、BC的中点.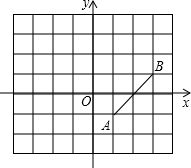 如图,线段AB两个端点的坐标分别为A(1,-1),B(3,1),将线段AB绕点O逆时针旋转90°到对应线段CD(点A与点C对应,点B与D对应).
如图,线段AB两个端点的坐标分别为A(1,-1),B(3,1),将线段AB绕点O逆时针旋转90°到对应线段CD(点A与点C对应,点B与D对应).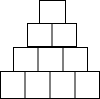 用若干个小立方块搭成的一个四层塔体的主视图,左视图是相同的图形,如图所示:
用若干个小立方块搭成的一个四层塔体的主视图,左视图是相同的图形,如图所示: