题目内容
20. 如图,AB为半圆O的直径,点C是OA的中点,CD⊥OA交半圆O于点D,点E是$\widehat{BD}$的中点,过点D作DP∥AE交BA的延长线于点P.求证:
如图,AB为半圆O的直径,点C是OA的中点,CD⊥OA交半圆O于点D,点E是$\widehat{BD}$的中点,过点D作DP∥AE交BA的延长线于点P.求证:(1)四边形PAED是平行四边形;
(2)PD是半圆O的切线.
分析 (1)根据CO与DO的数量关系,即可得出∠CDO的度数,进而求出∠AOD=60°,∠BOD=120°,∠AED=30°,点E是$\widehat{BD}$的中点,进而求出∠EAB=30°,即∠BAE=∠AED,得出ED∥AP,即可证得结论;
(2)利用点E是$\widehat{BD}$的中点,进而求出∠EAB=30°,即可得出∠AFO=90°,即可得出答案.
解答 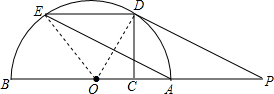 (1)解:连接OD、OE,
(1)解:连接OD、OE,
∵AB是半圆的直径,点O是圆心,点C是OA的中点,
∴2CO=DO,∠DCO=90°,
∴∠CDO=30°,
∴∠AOD=60°,
∴∠BOD=120°,∠AED=30°,
∵点E是$\widehat{BD}$的中点,
∴∠BOE=60°,
∴∠BAE=30°,
∴∠BAE=∠AED,
∴ED∥AP,
∵DP∥AE,
∴四边形PAED是平行四边形;
(2)证明:如图,∵点E是$\widehat{BD}$的中点,
∴$\widehat{DE}$=$\widehat{BE}$,
∵由(1)得∠AOD=60°,
∴∠DOB=120°,
∴∠BOE=60°,
∴∠EAB=30°,
∴∠AFO=90°,
∵DP∥AE,
∴PD⊥OD,
∴直线PD为⊙O的切线.
点评 此题主要考查了垂径定理以及圆周角定理和切线的判定定理等知识,根据已知得出∠AFO=90°是解题关键.

练习册系列答案
相关题目
10.如果+7%表示“增加7%”,那么“减少5%”可以记作( )
| A. | +2% | B. | -12% | C. | 5+% | D. | -5% |
5.到三角形三个顶点的距离相等的点一定是三角形( )的交点.
| A. | 三条角平分线 | B. | 三条边的垂直平分线 | ||
| C. | 三条高 | D. | 三条中线 |
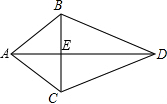 如图,已知AB=AC,BD=CD,AD与BC交于点E.请写出三个不同类型的正确结论.(不添加字母和辅助线,不要求证明)
如图,已知AB=AC,BD=CD,AD与BC交于点E.请写出三个不同类型的正确结论.(不添加字母和辅助线,不要求证明)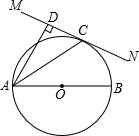 如图,己知AB为⊙O上直径,过C作直线MN,AD⊥MN于D,AC平分∠BAD,求证:MN与⊙O相切.
如图,己知AB为⊙O上直径,过C作直线MN,AD⊥MN于D,AC平分∠BAD,求证:MN与⊙O相切.