题目内容
15．
如图，已知点C是线段AB上任意一点，M、N分别是AC、BC的中点．（1）若AB=16，求MN的长；
（2）若AB=16，AC=6，求BN的长．
分析 （1）根据线段中点的性质，可得MC与AC的关系，CN与CB的关系，根据线段的差，可得答案；
（2）根据线段的和差，可得BC的长，根据线段中点的性质，可得答案．
解答 解：（1）由M、N分别是AC、BC的中点，得
MC=$\frac{1}{2}$AC，NC=$\frac{1}{2}$BC．
由线段和差，得
MN=MC+NC=$\frac{1}{2}$（AC+BC）=$\frac{1}{2}$×16=8；
（2）由线段的和差，得
BC=AB-AC=16-6=10，
由N是BC的中点，得
BN=$\frac{1}{2}$BC=$\frac{1}{2}$×10=5．
点评 本题考查了两点间的距离，利用了线段中点的性质，线段的和差．
练习册系列答案
浙江名校名师金卷系列答案
全优冲刺100分系列答案
相关题目
5．到三角形三个顶点的距离相等的点一定是三角形（ ）的交点．
| A． | 三条角平分线 | B． | 三条边的垂直平分线 | ||
| C． | 三条高 | D． | 三条中线 |
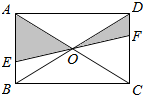如图所示，EF过矩形ABCD对角线的交点O，且分别交AB，CD于点E，F，若AB=3，BC=4，那么阴影部分的面积为（ ）
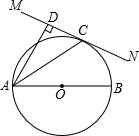如图，己知AB为⊙O上直径，过C作直线MN，AD⊥MN于D，AC平分∠BAD，求证：MN与⊙O相切．
如图，已知不等边三角形ABC．求作：作一个三角形，使它与△ABC有公共顶点C，并且与△ABC全等（不写作法，保留作图痕迹）．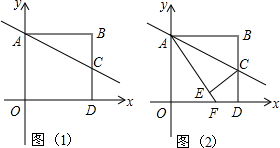
如图（1），四边形AODB是边长为2的正方形，C为BD的中点，以O为原点，OA、OD所在直线为坐标轴建立平面直角坐标系．