题目内容
17.若$\sqrt{10201}$=101,则$\sqrt{102.01}$等于( )| A. | 1.01 | B. | 10.1 | C. | 101 | D. | 1.0201 |
分析 依据被开放数向左或向右移动2n位,则对应的算术平方根向左或向右移动n位求解即可.γ
解答 解:∵若$\sqrt{10201}$=101,
∴$\sqrt{102.01}$等=10.1.
故选:B.
点评 本题主要考查的是算术平方根的性质,熟练掌握算术平方根的性质是解题的关键.

练习册系列答案
相关题目
8.如图a是长方形纸带,AB=2,AD=8,AE=CF,将纸带沿EF折叠成图b,再沿BF折叠成图c,若图c中BE∥DG,则AE的长是( )


| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{6-\sqrt{6}}{2}$ | D. | $\frac{6-\sqrt{6}}{2}$或$\frac{6+\sqrt{6}}{2}$ |
2.五一节期间,电器市场火爆,某商店需要购进一批电视机和洗衣机,根据市场调查,电视机与洗衣机的进价和售价如下表:
若该商店计划电视机和洗衣机共100台,设购进电视机x台,获得的总利润y元.
(1)求出y与x的函数关系;
(2)已知商店最多筹集资金161800元,求购进多少台电视机,才能使商店销售购进的电视机与洗衣机完毕后获得的利润最多?并求出最多利润.(利润=售价-进价)
| 类别 | 电视机 | 洗衣机 |
| 进价(元/台) | 1800 | 1500 |
| 售价(元/台) | 2000 | 1600 |
(1)求出y与x的函数关系;
(2)已知商店最多筹集资金161800元,求购进多少台电视机,才能使商店销售购进的电视机与洗衣机完毕后获得的利润最多?并求出最多利润.(利润=售价-进价)
6. 如图,直线a∥b,直线l分别与直线a,b相交于点P,Q,PA垂直于l于点P.若∠1=64°,则∠2的度数为( )
如图,直线a∥b,直线l分别与直线a,b相交于点P,Q,PA垂直于l于点P.若∠1=64°,则∠2的度数为( )
 如图,直线a∥b,直线l分别与直线a,b相交于点P,Q,PA垂直于l于点P.若∠1=64°,则∠2的度数为( )
如图,直线a∥b,直线l分别与直线a,b相交于点P,Q,PA垂直于l于点P.若∠1=64°,则∠2的度数为( )| A. | 26° | B. | 30° | C. | 36° | D. | 64° |
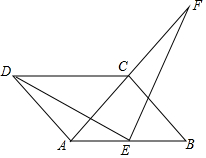 如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上的一点.
如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上的一点.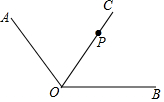 如图,已知OC平分∠AOB,点P是OC上一点,作图:过点P画PE⊥OA,PF⊥OB,垂足分别为点E和点F,并完成填空:PE=PF(填“>”或“=”“<”).
如图,已知OC平分∠AOB,点P是OC上一点,作图:过点P画PE⊥OA,PF⊥OB,垂足分别为点E和点F,并完成填空:PE=PF(填“>”或“=”“<”).