题目内容
19.杨光调查了他们班50名同学各自家庭的人均日用水量(单位:升),结果如下:55 42 50 48 42 35 38 39 40 51 47 52 50 42 43 47 52 48 54 52 38 42 60 52 41 46 35 47 53 48 52 47 50 49 57 43 40 44 52 50 49 37 46 42 62 58 46 48 39 60
请根据以上数据绘制频数分布表和频数分布直方图,并回答下列问题:
(注意:请按组距为4,组数为7绘制频数分布表和频数分布直方图.)
(1)家庭人均日用水量在哪个范围的家庭最多?这个范围的家庭占全班家庭的百分之几?
(2)如果每人每天节约用水8升,按全班50人计算,一年(按365天计算)可节约用水多少吨?按生活基本日均需水量50升的标准计算,这些水可供1个人多长时间的生活用水?
分析 (1)根据绘制的频数分布表和频数分布直方图,即可得到家庭人均日用水量在47≤x<51范围的家庭最多,以及这个范围的家庭占全班家庭的百分比;
(2)根据每人每天节约用水8升,按全班50人计算,一年按365天计算,即可得到节约的用水量,按生活基本日均需水量50升的标准计算,即可得到这些水可供1个人生活的时间.
解答 解:计算最大值与最小值的差:62-35=27;
决定组距和组数:取组距为4,由于27÷4=6.75,因此要将整个数据分为7组,
用x(升)表示人均日用水量,则所分的组为:
35≤x<39,39≤x<43,43≤x<47,47≤x<51,51≤x<55,55≤x<59,59≤x<63,
列频数分布表: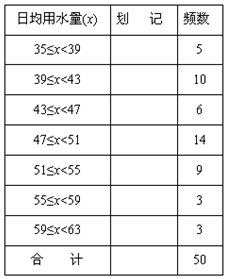
画频数分布直方图: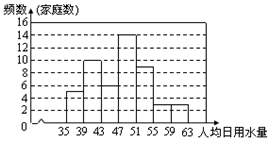
根据频数分布表和频数分布直方图可得:
(1)家庭人均日用水量在47≤x<51范围的家庭最多,
这个范围的家庭占全班家庭的百分比为:$\frac{14}{50}$×100%=28%;
(2)一年(按365天计算)可节约用水:8×50×365÷1000=146(吨),
按生活基本日均需水量50升的标准计算,这些水可供1个人生活:146×1000÷50÷365=8(年).
点评 本题主要考查了频数分布表和频数分布直方图的应用,在统计数据时,经常把数据按照不同的范围分成几个组,分成的组的个数称为组数,每一组两个端点的差称为组距,称这样画出的统计图表为频数分布表.画频率分布直方图的步骤:(1)计算极差.(2)决定组距与组数.(3)确定分点,将数据分组.(4)列频率分布表.(5)绘制频率分布直方图.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.某快餐店共有10名员工,所有员工工资的情况如下表:
请解答下列问题:
(1)餐厅所有员工的平均工资是4350;所有员工工资的中位数是2000.
(2)用平均数还是用中位数描述该餐厅员工工资的一般水平比较恰当?
(3)去掉店长和厨师甲的工资后,其他员工的平均工资是多少?它是否也能反映该快餐店员工工资的一般水平?
| 人员 | 店长 | 厨师甲 | 厨师乙 | 会计 | 服务员甲 | 服务员乙 | 勤杂工 |
| 人数 | 1 | 1 | 1 | 1 | 1 | 3 | 2 |
| 工资额 | 20000 | 7000 | 4000 | 2500 | 2200 | 1800 | 1200 |
(1)餐厅所有员工的平均工资是4350;所有员工工资的中位数是2000.
(2)用平均数还是用中位数描述该餐厅员工工资的一般水平比较恰当?
(3)去掉店长和厨师甲的工资后,其他员工的平均工资是多少?它是否也能反映该快餐店员工工资的一般水平?
4.下列计算结果正确的是( )
| A. | (a3)2=a6 | B. | (-3a2)2=6a4 | C. | (-a2)3=a6 | D. | (-$\frac{1}{2}$ab2)3=$\frac{1}{8}$a3b6 |
8.如图a是长方形纸带,AB=2,AD=8,AE=CF,将纸带沿EF折叠成图b,再沿BF折叠成图c,若图c中BE∥DG,则AE的长是( )


| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{6-\sqrt{6}}{2}$ | D. | $\frac{6-\sqrt{6}}{2}$或$\frac{6+\sqrt{6}}{2}$ |
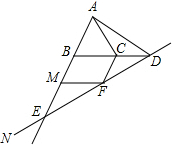 如图,在等边△ABC中,点D在BC的延长线上,连接AD,∠ADN=60°,直线DN交射线AB于点E,过点C作CF∥AB交直线DN于点F,过点F作MF∥BC交射线AB于点M.
如图,在等边△ABC中,点D在BC的延长线上,连接AD,∠ADN=60°,直线DN交射线AB于点E,过点C作CF∥AB交直线DN于点F,过点F作MF∥BC交射线AB于点M.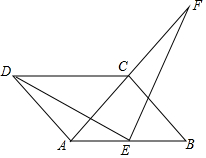 如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上的一点.
如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上的一点.