题目内容
12.若|x-y-3z|+(y-1)2+|2x-y|=0,则x+y+z的值为$\frac{4}{3}$.分析 根据非负数的和为零,可得方程组,根据解方程组,可得答案.
解答 解:由题意,得
$\left\{\begin{array}{l}{x-y-3z=0}\\{y-1=0}\\{2x-y=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=1}\\{z=-\frac{1}{6}}\end{array}\right.$,
x+y+z=$\frac{1}{2}$+1-$\frac{1}{6}$=$\frac{4}{3}$,
故答案为:$\frac{4}{3}$.
点评 本题考查了解二元一次方程组,利用非负数的和为零得出方程组是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.将分式$\frac{6m{n}^{3}}{4{m}^{3}n}$化成最简分式的结果正确的是( )
| A. | $\frac{6{n}^{2}}{4{m}^{2}}$ | B. | $\frac{6n}{4m}$ | C. | $\frac{3{n}^{2}}{2{m}^{2}}$ | D. | $\frac{3n}{2m}$ |
4.下列计算结果正确的是( )
| A. | (a3)2=a6 | B. | (-3a2)2=6a4 | C. | (-a2)3=a6 | D. | (-$\frac{1}{2}$ab2)3=$\frac{1}{8}$a3b6 |
2.五一节期间,电器市场火爆,某商店需要购进一批电视机和洗衣机,根据市场调查,电视机与洗衣机的进价和售价如下表:
若该商店计划电视机和洗衣机共100台,设购进电视机x台,获得的总利润y元.
(1)求出y与x的函数关系;
(2)已知商店最多筹集资金161800元,求购进多少台电视机,才能使商店销售购进的电视机与洗衣机完毕后获得的利润最多?并求出最多利润.(利润=售价-进价)
| 类别 | 电视机 | 洗衣机 |
| 进价(元/台) | 1800 | 1500 |
| 售价(元/台) | 2000 | 1600 |
(1)求出y与x的函数关系;
(2)已知商店最多筹集资金161800元,求购进多少台电视机,才能使商店销售购进的电视机与洗衣机完毕后获得的利润最多?并求出最多利润.(利润=售价-进价)
 (1)计算:-3tan30°+$\sqrt{12}$
(1)计算:-3tan30°+$\sqrt{12}$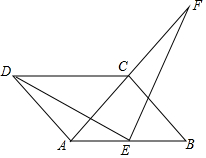 如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上的一点.
如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上的一点.