题目内容
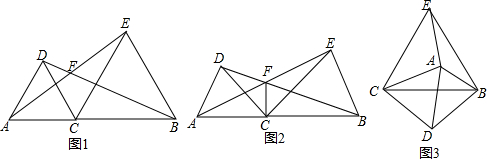
3.发现:如图1,在边长为a米的正方形草坪上修建一条宽为b米的道路,为求剩余草坪的面积,小明想出了两种方法.方法(1):用正方形的面积减去中间道路的面积,求得剩余草坪的面积为a2-ab;方法(2):如图2,把如图1的道路右侧阴影向左平移,与左边的阴影部分拼凑成如图3的小长方形,则求得剩余面积为a(a-b).由此我们可得出等式a2-ab=a(a-b).
思考:
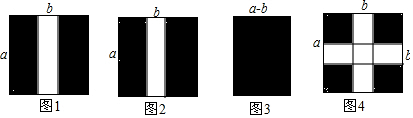
如图4,在边长为a米的正方形的草坪上修建两条宽为b米的道路,小亮也仿照小明方法,求出了剩余草坪的面积.结果如下:
方法①:a2+b2-2ab;
方法②:(a-b)2.(用含a,b的代数式写出结果)
探索:
从小亮计算草坪面积的不同方法中,请你写出(a-b)2与a2+b2,ab三个代数式之间的等量关系:(a-b)2=a2+b2-2ab.
应用:
根据探索中的等量关系,解决如下问题:m2+n2=9,mn=-8,求m-n的值.
分析 直接利用已知图形的边长结合其面积求法得出答案.
解答 解:由此我们可得出等式:a2-ab=a(a-b);
剩余草坪的面积为:a2+b2-2ab;
剩余草坪的面积为:(a-b)2;
(a-b)2与a2+b2,ab三个代数式之间的等量关系:(a-b)2=a2+b2-2ab;
∵m2+n2=9,mn=-8,
∴m2+n2-2mn=9+16=25,
∴(m-n)2=25,
∴m-n=±5.
故答案为:a2-ab=a(a-b);a2+b2-2ab;(a-b)2;(a-b)2=a2+b2-2ab.
点评 此题主要考查了完全平方公式的几何背景,正确利用完全平方公式是解题关键.

练习册系列答案
相关题目
13. 如图,坐标系中抛物线是函数y=ax2+bx+c的图象,则下列式子能成立的是( )
如图,坐标系中抛物线是函数y=ax2+bx+c的图象,则下列式子能成立的是( )
 如图,坐标系中抛物线是函数y=ax2+bx+c的图象,则下列式子能成立的是( )
如图,坐标系中抛物线是函数y=ax2+bx+c的图象,则下列式子能成立的是( )| A. | abc>0 | B. | a+b+c<0 | C. | b<a+c | D. | 4a+2b+c>0 |
11.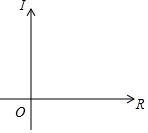 张华同学在一次做电学实验时,记录下电流I(安)与电阻R(欧)有如表对应关系:
张华同学在一次做电学实验时,记录下电流I(安)与电阻R(欧)有如表对应关系:
通过描点连线,观察并求出I与R之间的函数关系式.
 张华同学在一次做电学实验时,记录下电流I(安)与电阻R(欧)有如表对应关系:
张华同学在一次做电学实验时,记录下电流I(安)与电阻R(欧)有如表对应关系:| R | … | 2 | 4 | 8 | 10 | 16 | … |
| I | … | 16 | 8 | 4 | 3.2 | 2 | … |
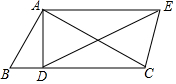 如图三角板ABC中,∠BAC=90°,∠B=60°,把△ABC绕点A逆时针旋转30°得到△ADE,连接CE,则∠CED=45°.
如图三角板ABC中,∠BAC=90°,∠B=60°,把△ABC绕点A逆时针旋转30°得到△ADE,连接CE,则∠CED=45°.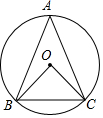 如图,在⊙O中,AB=AC,∠ABC=70°.∠BOC=80°.
如图,在⊙O中,AB=AC,∠ABC=70°.∠BOC=80°.