题目内容
3.计算:(1)$\sqrt{9}$-$\sqrt{(-6)^{2}}$-$\root{3}{-27}$
(2)|$\sqrt{6}$-$\sqrt{3}$|-|3-$\sqrt{6}$|
(3)求出x的值:x2-$\frac{121}{49}$=0.
分析 (1)原式利用算术平方根,立方根定义,以及二次根式性质计算即可得到结果;
(2)原式利用绝对值的代数意义化简,计算即可得到结果;
(3)方程整理后,利用平方根定义开方即可求出x的值.
解答 解:(1)原式=3-6+3=0;
(2)原式=$\sqrt{6}$-$\sqrt{3}$-3+$\sqrt{6}$=2$\sqrt{6}$-$\sqrt{3}$-3;
(3)方程整理得:x2=$\frac{121}{49}$,
开方得:x=±$\frac{11}{7}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.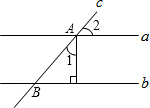 如图,直线a∥b,直线c与直线a、b分别相交于点A,B,AD⊥b,垂足为D,若∠1=47°,则∠2=( )
如图,直线a∥b,直线c与直线a、b分别相交于点A,B,AD⊥b,垂足为D,若∠1=47°,则∠2=( )
 如图,直线a∥b,直线c与直线a、b分别相交于点A,B,AD⊥b,垂足为D,若∠1=47°,则∠2=( )
如图,直线a∥b,直线c与直线a、b分别相交于点A,B,AD⊥b,垂足为D,若∠1=47°,则∠2=( )| A. | 57° | B. | 53° | C. | 47° | D. | 43° |
8.在代数式$\frac{{x}^{2}+1}{2}$、$\frac{3xy}{π}$、$\frac{3}{x+y}$、a$+\frac{1}{m}$中,分式的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
12.已知A(x1,y1)是一次函数y=-x+b+1图象上一点,若x1<0,y1<0,则b的取值范围是( )
| A. | b<0 | B. | b>0 | C. | b>-1 | D. | b<-1 |