题目内容
15.计算或化简(1)$\frac{3}{m}$$+\frac{m-15}{5m}$
(2)计算:$\frac{{x}^{2}-4}{{x}^{2}-4x+4}$$÷\frac{x+2}{x+1}$-$\frac{x}{x-2}$.
分析 (1)原式通分并利用同分母分式的加法法则计算,约分即可得到结果;
(2)原式第一项利用除法法则变形,约分后利用同分母分式的减法法则计算即可得到结果.
解答 解:(1)原式=$\frac{15}{5m}$+$\frac{m-15}{5m}$=$\frac{15+m-15}{5m}$=$\frac{m}{5m}$=$\frac{1}{5}$;
(2)原式=$\frac{(x+2)(x-2)}{(x-2)^{2}}$•$\frac{x+1}{x+2}$-$\frac{x}{x-2}$=$\frac{x+1}{x-2}$-$\frac{x}{x-2}$=$\frac{1}{x-2}$.
点评 此题考查了分式的混合运算,以及分式的加减,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
6.绝对值小于6且大于3的整数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.我省深入推进千万亩森林增长工程,2015年新造林226.3万亩,其中226.3万用科学记数法表示为( )
| A. | 226.3×104 | B. | 2.263×105 | C. | 2.263×106 | D. | 2.263×107 |
5.在下列多项式的乘法中,不能用平方差公式计算的是( )
| A. | (c2-d2)(d2+c2) | B. | (x3-y3)(x3+y3) | C. | (-a-b)(a-b) | D. | (m-n)(-m+n) |
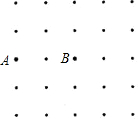 如图,由25个点构成的5×5的正方形点阵中,横纵方向相邻的两点之间的距离都是1个单位.定义:由点阵中四个点为顶点的平行四边形叫阵点平行四边形.图中以A,B为顶点,面积为2的阵点平行四边形的个数为9个.
如图,由25个点构成的5×5的正方形点阵中,横纵方向相邻的两点之间的距离都是1个单位.定义:由点阵中四个点为顶点的平行四边形叫阵点平行四边形.图中以A,B为顶点,面积为2的阵点平行四边形的个数为9个.