题目内容
如图是某田径场地椭圆式跑道的示意图:直道的长度为85.96米,第一条半圆形跑道的直径为72.6米,每条跑道的宽是1.25米,共8道.
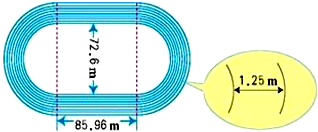
(1)第一条跑道的总面积是多少平方米?(精确度到0.01平方米)
(2)小明在这个场地上练习骑自行车,他的自行车有关数据如下:
前齿轮齿数:26 后齿轮齿数:16 车轮直径:66cm
假设他始终在最外道骑行,每分钟平均蹬25圈,他骑行1周大约需要几分钟?(π取3.14159)

(1)第一条跑道的总面积是多少平方米?(精确度到0.01平方米)
(2)小明在这个场地上练习骑自行车,他的自行车有关数据如下:
前齿轮齿数:26 后齿轮齿数:16 车轮直径:66cm
假设他始终在最外道骑行,每分钟平均蹬25圈,他骑行1周大约需要几分钟?(π取3.14159)
考点:一元一次方程的应用
专题:
分析:(1)直接求出直道部分的面积和弯道部分面积进而得出答案;
(2)首先求出每分钟骑车的距离,进而求出跑道周长,进而得出等式求出即可.
(2)首先求出每分钟骑车的距离,进而求出跑道周长,进而得出等式求出即可.
解答:解:(1)由题意可得:直道部分的面积为:85.96×1.25×2=214.9(m2),
弯道部分面积为:π×[(
+1.25)2-(
)2]≈290.01(m2),
故214.9+290.01=504.91(m2).
答:第一条跑道的总面积是504.91平方米;
(2)∵前齿轮齿数:26,后齿轮齿数:16,每分钟平均蹬25圈,
∴每分钟车轮转动:
=40.625(圈),
∵车轮直径:66cm,
∴车轮的周长为:π×66cm≈2.073m,
故每分钟车轮转动:2.073×40.625≈84.22(m)
弯道部分的周长为:π(72.6+16×1.25)≈290.91(m),
直道部分长度为:85.96×2=171.92(m),
故最外道的长为:290.91+171.92=462.83(m),
设他骑行1周大约需要x分钟,根据题意可得:
84.22x=462.83,
解得:x≈5.50,
答:他骑行1周大约需要5.50分钟.
弯道部分面积为:π×[(
| 72.6 |
| 2 |
| 72.6 |
| 2 |
故214.9+290.01=504.91(m2).
答:第一条跑道的总面积是504.91平方米;
(2)∵前齿轮齿数:26,后齿轮齿数:16,每分钟平均蹬25圈,
∴每分钟车轮转动:
| 26×25 |
| 16 |
∵车轮直径:66cm,
∴车轮的周长为:π×66cm≈2.073m,
故每分钟车轮转动:2.073×40.625≈84.22(m)
弯道部分的周长为:π(72.6+16×1.25)≈290.91(m),
直道部分长度为:85.96×2=171.92(m),
故最外道的长为:290.91+171.92=462.83(m),
设他骑行1周大约需要x分钟,根据题意可得:
84.22x=462.83,
解得:x≈5.50,
答:他骑行1周大约需要5.50分钟.
点评:此题主要考查了一元一次方程的应用,根据题意得出每分钟骑自行车的距离是解题关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
 如图,在平面直角坐标系中,直线y=-2x+42交x轴于点A,交直线y=x交于点B.抛物线y=ax2-2x+c分别交线段AB、OB于点C、D,点C和点D的横坐标分别为16和4.
如图,在平面直角坐标系中,直线y=-2x+42交x轴于点A,交直线y=x交于点B.抛物线y=ax2-2x+c分别交线段AB、OB于点C、D,点C和点D的横坐标分别为16和4.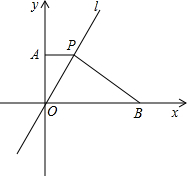 如图,在直角坐标系中,直线l经过原点O,点P是第一象限内直线l上的点,过点P作PA垂直y轴于点A,点P的横坐标为1,点B的横坐标为5,PB⊥PO,交x轴于点B.
如图,在直角坐标系中,直线l经过原点O,点P是第一象限内直线l上的点,过点P作PA垂直y轴于点A,点P的横坐标为1,点B的横坐标为5,PB⊥PO,交x轴于点B.