题目内容
一工地计划租用甲、乙两辆车清理淤泥,从运输量来估算:乙车单独施工完成此项任务比甲车单独施工完成此项任务多用10天,且乙车单独施工45天和甲车单独施工30天的工作量相同.
(1)甲、乙两车单独完成任务分别需要多少天?
(2)已知两车合运共需租金72000元,甲车每天的租金比乙车每天的租金多1500元.试问:租甲乙两车、单独租甲车、单独租乙车这三种方案中,哪一种租金最少?请说明理由.
(1)甲、乙两车单独完成任务分别需要多少天?
(2)已知两车合运共需租金72000元,甲车每天的租金比乙车每天的租金多1500元.试问:租甲乙两车、单独租甲车、单独租乙车这三种方案中,哪一种租金最少?请说明理由.
考点:分式方程的应用,一元一次方程的应用
专题:
分析:(1)设甲车单独完成任务需要x天,则乙单独完成需要(x+10)天,根据乙车单独施工45天和甲车单独施工30天的工作量相同列出方程,解方程即可;
(2)先求出甲乙车合运需要1÷(
+
)=12天,再设乙车每天租金为a元,则每天甲车租金为(1500+a)元,根据两车合运共需租金72000元,列出方程,解方程求出a的值,再分别求出租甲乙两车、单独租甲车、单独租乙车这三种方案的租金,比较即可.
(2)先求出甲乙车合运需要1÷(
| 1 |
| 20 |
| 1 |
| 30 |
解答:解:(1)设甲车单独完成任务需要x天,则乙单独完成需要(x+10)天,
根据题意可得:
=
,
解得:x=20.
经检验,x=20是原方程的根.
所以x=20,x+10=30.
答:甲车单独完成需要20天,乙车单独完成需要30天;
(2)甲乙车合运需要1÷(
+
)=12天,
设乙车每天租金为a元,则每天甲车租金为(1500+a)元,
根据题意得,12a+12(1500+a)=72000,
解得:a=2250,
a+1500=3750.
①租甲乙两车需要费用为:72000元;
②单独租甲车的费用为:20×3750=75000元;
③单独租乙车需要的费用为:30×2250=67500元.
综上可得,单独租乙车租金最少.
根据题意可得:
| 45 |
| 10+x |
| 30 |
| x |
解得:x=20.
经检验,x=20是原方程的根.
所以x=20,x+10=30.
答:甲车单独完成需要20天,乙车单独完成需要30天;
(2)甲乙车合运需要1÷(
| 1 |
| 20 |
| 1 |
| 30 |
设乙车每天租金为a元,则每天甲车租金为(1500+a)元,
根据题意得,12a+12(1500+a)=72000,
解得:a=2250,
a+1500=3750.
①租甲乙两车需要费用为:72000元;
②单独租甲车的费用为:20×3750=75000元;
③单独租乙车需要的费用为:30×2250=67500元.
综上可得,单独租乙车租金最少.
点评:本题考查分式方程与一元一次方程的应用,分析题意,找到合适的等量关系是解决问题的关键.

练习册系列答案
相关题目
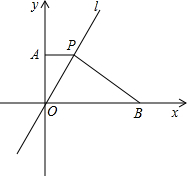 如图,在直角坐标系中,直线l经过原点O,点P是第一象限内直线l上的点,过点P作PA垂直y轴于点A,点P的横坐标为1,点B的横坐标为5,PB⊥PO,交x轴于点B.
如图,在直角坐标系中,直线l经过原点O,点P是第一象限内直线l上的点,过点P作PA垂直y轴于点A,点P的横坐标为1,点B的横坐标为5,PB⊥PO,交x轴于点B.
 面积为1的正方形ABCD中,F是BC的中点,BD、AF交于E点,求正方形被分成四部分的面积.
面积为1的正方形ABCD中,F是BC的中点,BD、AF交于E点,求正方形被分成四部分的面积.