题目内容
18. 如图,△AOB为等边三角形,点B的坐标为(-4,0),过点C(4,0)作直线l交AO于D,交AB于E,点E在某反比例函数图象上,当△ADE和△DCO的面积相等时,那么该反比例函数的解析式为y=-$\frac{{3\sqrt{3}}}{x}$.
如图,△AOB为等边三角形,点B的坐标为(-4,0),过点C(4,0)作直线l交AO于D,交AB于E,点E在某反比例函数图象上,当△ADE和△DCO的面积相等时,那么该反比例函数的解析式为y=-$\frac{{3\sqrt{3}}}{x}$.
分析 根据等边三角形的性质和勾股定理求得AE的长,再求出点E的坐标,从而求出k值,得出解析式.
解答 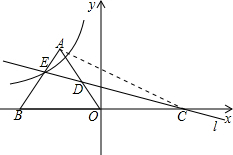 解:连接AC.
解:连接AC.
∵点B的坐标为(-4,0),△AOB为等边三角形,
∵AO=OC=4,
∴∠OCA=∠OAC,
∵∠AOB=60°,
∴∠ACO=30°,∠B=60°,
∴∠BAC=90°,
∴点A的坐标为(-2,2$\sqrt{3}$),
∵S△ADE=S△DCO,S△AEC=S△ADE+S△ADC,S△AOC=S△DCO+S△ADC,
∴S△AEC=S△AOC=$\frac{1}{2}$×AE•AC=$\frac{1}{2}$•CO•2$\sqrt{3}$,
即$\frac{1}{2}$•AE•4$\sqrt{3}$=$\frac{1}{2}×4×2\sqrt{3}$,
∴AE=2.
∴E点为AB的中点(-3,$\sqrt{3}$)
把E点(-3,$\sqrt{3}$)代入y=$\frac{k}{x}$,
k=-3$\sqrt{3}$.
所以反比例函数解析式为y=-$\frac{{3\sqrt{3}}}{x}$,
故答案为:-$\frac{{3\sqrt{3}}}{x}$.
点评 本题考查了本题考查了反比例函数系数k的几何意义,用待定系数法求反比例函数的解析式,等边三角形的性质、三角形的面积,知道|k|也是该点到两坐标轴的垂线段与两坐标轴围成的矩形面积是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.点P(6,8)到原点的距离为( )
| A. | 6 | B. | 8 | C. | 10 | D. | 以上都不对 |
9.以长为5cm,6cm,8cm,11cm的四条线段中的三条线段为边可以画出( )个三角形.
| A. | 4 | B. | 2 | C. | 1 | D. | 3 |
3.如果3x=m,3y=n,那么3x-y等于( )
| A. | m+n | B. | m-n | C. | mn | D. | $\frac{m}{n}$ |