题目内容
15.小明想要测量公园内一座楼CD的高度.他先在A处测得楼顶C的仰角α=30°,再向楼的方向直行10米到达B处,又测得楼顶C的仰角β=60°,若小明的眼睛到地面的高度AE为1.60米,请你帮助他计算出这座楼CD的高度(结果精确到0.1米).参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{5}$≈2.24.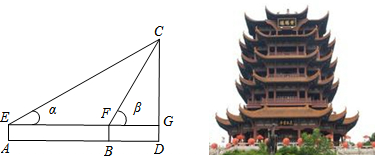
分析 由α=30°,β=60°,可求得∠ECF=α=30°,然后由等角对等边,可得CF=EF=10米,则可求得CG的长,继而求得这座楼CD的高度.
解答 解:∵α=30°,β=60°,
∴∠ECF=β-α=30°.
∴CF=EF=10米,
在Rt△CFG中,CG=CF•cosβ=5$\sqrt{3}$(米),
∴CD=CG+GD=5$\sqrt{3}$+1.60≈10.3( 米).
答:这座楼的高度约为10.3米.
点评 本题考查解直角三角形的应用-仰角俯角问题.注意能借助仰角构造直角三角形并解直角三角形是解此题的关键.

练习册系列答案
相关题目
7.下列事件中,是必然事件的是( )
| A. | 明天太阳从东方升起 | |
| B. | 射击运动员射击一次,命中靶心 | |
| C. | 随意翻到一本书的某页,这页的页码是奇数 | |
| D. | 经过有交通信号灯的路口,遇到红灯 |
4.已知M(1,-2),N(-3,-2),则直线MN与x轴,y轴的位置关系分别为( )
| A. | 相交,相交 | B. | 平行,平行 | C. | 垂直,平行 | D. | 平行,垂直 |
 如图,有一半圆形桥拱,拱的跨度AB=40米,那么桥拱的弧长为62.8米.(结果精确到0.1米)
如图,有一半圆形桥拱,拱的跨度AB=40米,那么桥拱的弧长为62.8米.(结果精确到0.1米)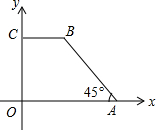 如图,在平面直角坐标系中有一个四边形OABC,其中CB∥x轴,OC=3,BC=2,∠OAB=45°.
如图,在平面直角坐标系中有一个四边形OABC,其中CB∥x轴,OC=3,BC=2,∠OAB=45°.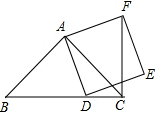 已知:在△ABC中,∠BAC=90°,∠ABC=45°,点D为线段BC上一动点(点D不与B、C重合),以AD为边向右作正方形ADEF,连接FC,探究:无论点D运动到何处,线段FC、DC、BC三者的长度之间都有怎样的数量关系?请予以证明.
已知:在△ABC中,∠BAC=90°,∠ABC=45°,点D为线段BC上一动点(点D不与B、C重合),以AD为边向右作正方形ADEF,连接FC,探究:无论点D运动到何处,线段FC、DC、BC三者的长度之间都有怎样的数量关系?请予以证明.