题目内容
10.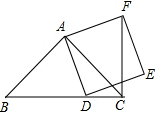 已知:在△ABC中,∠BAC=90°,∠ABC=45°,点D为线段BC上一动点(点D不与B、C重合),以AD为边向右作正方形ADEF,连接FC,探究:无论点D运动到何处,线段FC、DC、BC三者的长度之间都有怎样的数量关系?请予以证明.
已知:在△ABC中,∠BAC=90°,∠ABC=45°,点D为线段BC上一动点(点D不与B、C重合),以AD为边向右作正方形ADEF,连接FC,探究:无论点D运动到何处,线段FC、DC、BC三者的长度之间都有怎样的数量关系?请予以证明.
分析 根据正方形的性质、全等三角形的判定定理证明△BAD≌△FAC,根据全等三角形的性质证明即可.
解答 解:无论点D运动到何处,都有BC=FC+DC,
理由如下:
在△ABC中,∵∠BAC=90°,∠ABC=45°,
∴∠ACB=45°,
∴AB=AC,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAD+∠DAC=∠FAC+∠DAC=90°,
∴∠BAD=∠FAC,
∴△BAD≌△FAC(SAS)
∴BD=FC,
又∵BC=BD+DC,
∴BC=FC+DC.
点评 本题考查的是正方形的性质,掌握全等三角形的判定定理和性质定理、正方形的性质定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知一个多项式与3x2+8x的和等于3x2+2x+4,则这个多项式是( )
| A. | 6x+4 | B. | -6x+4 | C. | 6x-4 | D. | -6x-4 |
1.一个事件的概率不可能是( )
| A. | $\frac{3}{2}$ | B. | 0 | C. | 1 | D. | $\frac{1}{3}$ |
18.已知函数y=(m+1)x${\;}^{{m}^{2}-3}$是正比例函数,且图象在第二、四象限内,则m的值是( )
| A. | 2 | B. | -2 | C. | ±2 | D. | -$\frac{1}{2}$ |
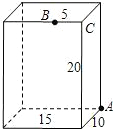 如图,长方体的长为15cm,宽为10cm,高为20cm,点B距离C点5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,徐亚爬行的最短距离是25cm.
如图,长方体的长为15cm,宽为10cm,高为20cm,点B距离C点5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,徐亚爬行的最短距离是25cm.
 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).