题目内容
2.小明现有甲乙两种不同型号的圆环,圆环的外圆直径与环宽如图1所示,现将同一型号的圆环分别扣在一起并拉紧成一条长链,已知甲型号圆环的外圆直径是8cm,环宽1cm(1)探究发现:
将两个甲型号圆环扣在一起并拉紧,其长度为14cm;
将3个甲型号圆环扣在一起并拉紧,其长度为20cm;

如果将4个甲型号圆环扣在一起并拉紧,其长度为26cm;
如果将n个甲型号圆环扣在一起并拉紧,其长度为(6n+2)cm(用含n的式子表示).
(2)实践应用:
①若3个乙型号圆环相扣并拉紧后长度是28cm,5个乙型号圆环相扣并拉紧后长度是44cm,求乙型号圆环的外圆直径和环宽;
②在①的条件下,小明用若干个甲型号圆环制作成一条长链,再用若干个乙型号圆环制作成一条长链,已知甲型号圆环比乙型号圆环多5个,且由甲型号圆环制作的长链比用乙型号圆环制作的长链更长,那么小明最多有多少个甲型号圆环?
分析 (1)由于圆环的外圆直径是8厘米,环宽1厘米,所以内圆直径是6厘米.
①如果把这样的4个圆环扣在一起并拉紧,那么长度为4个内圆直径+2个环宽;
②如果用n个这样的圆环相扣并拉紧,那么长度为n个内圆直径+2个环宽;
(2)①设乙型号圆环的外圆直径为xcm,环宽为ycm,利用3个乙型号圆环的长度是28cm,5个乙型号圆环的长度是44cm,分别得出方程即可求出;
②设乙型号圆环有m个,则甲型号圆环有(m+5)个,根据甲型号圆环制作的长链比用乙型号圆环制作的长链更长列出不等式求解即可.
解答 解:(1)①结合图形可知:
把这样的4个圆环扣在一起并拉紧,那么长度为4个内圆直径+2个环宽,
∴长度为6×4+2=26cm,
②根据以上规律可知:如果用n个这样的圆环相扣并拉紧,长度为:6n+2;
故答案为:26,(6n+2);
(2)①设乙型号圆环的外圆直径为xcm,环宽为ycm,
则根据题意得:$\left\{\begin{array}{l}{3x-4y=28}\\{5x-8y=44}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=12}\\{y=2}\end{array}\right.$.
答:乙型号圆环的外圆直径为12cm,环宽为2cm.
②设乙型号圆环有m个,则甲型号圆环有(m+5)个,依题意有
6(m+5)+2>8m+4,
解得m<17,
则m+5<22,
∵m为整数,
∴小明最多有21个甲型号圆环.
点评 此题主要考查了应用类问题,列代数式以及二元一次方程组的应用和一元一次不等式的应用,找到所求式子的等量关系的规律是解决问题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
7.等腰三角形一腰上的高与另一腰的夹角为40°,则其顶角为( )
| A. | 50° | B. | 130° | C. | 50°或130° | D. | 55°或130° |
12. 如图所示,OC平分∠AOB,OD平分∠AOC,且∠COD=25°,则∠AOB等于( )
如图所示,OC平分∠AOB,OD平分∠AOC,且∠COD=25°,则∠AOB等于( )
 如图所示,OC平分∠AOB,OD平分∠AOC,且∠COD=25°,则∠AOB等于( )
如图所示,OC平分∠AOB,OD平分∠AOC,且∠COD=25°,则∠AOB等于( )| A. | 50° | B. | 75° | C. | 100° | D. | 20° |
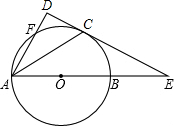 如图,已知AB是⊙O的直径,直线CE与⊙O相切于点C,交AB的延长线交于点E.作AD⊥CE,垂足为D,连接AC.求证:AC平分∠DAB.
如图,已知AB是⊙O的直径,直线CE与⊙O相切于点C,交AB的延长线交于点E.作AD⊥CE,垂足为D,连接AC.求证:AC平分∠DAB.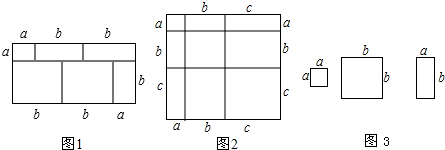
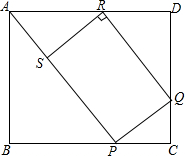 如图所示,矩形ABCD中,AB=1,BC=x,P,Q分别是BC,CD,DA上的点,且∠BAP=45°,CP=CQ,RQ∥AP.RS⊥AP于点S.
如图所示,矩形ABCD中,AB=1,BC=x,P,Q分别是BC,CD,DA上的点,且∠BAP=45°,CP=CQ,RQ∥AP.RS⊥AP于点S. 如图,C、D是线段AB上的两点,点D是AC中点,AB=10,AD=4,则DB=6.
如图,C、D是线段AB上的两点,点D是AC中点,AB=10,AD=4,则DB=6.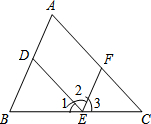 如图,在下列解答中,填空或填写适当的理由:
如图,在下列解答中,填空或填写适当的理由: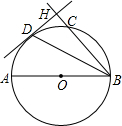 如图,已知AB为⊙O的直径,弦BD平分∠ABH,过点D作DH⊥BH于点H,BH交⊙O于点C.
如图,已知AB为⊙O的直径,弦BD平分∠ABH,过点D作DH⊥BH于点H,BH交⊙O于点C.