题目内容

边长2cm，3cm，4cm的三角形的面积是
 
．
考点：勾股定理
专题：
分析：如图，过A点作AD⊥BC于D．根据勾股定理得到关于底边为4cm的高AD的方程，解方程求出高AD，再根据三角形面积公式即可得到三角形的面积．
解答：解：如图，过A点作AD⊥BC于D．
根据勾股定理可得
22-AD2
+
32-AD2
=4，
解得AD=±
3
15
8
（负值舍去），
经检验，AD=
3
15
8
是原方程的解，
4×
3
15
8
÷2=
3
15
4
（cm2）
答：三角形的面积是
3
15
4
cm2．
故答案为：
3
15
4
cm2．
点评：考查了勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．本题关键是得到高AD的长．
练习册系列答案
相关题目
关于x的反比例函数y=
a+4
x
的图象如图，A、P为该图象上的点，且关于原点成中心对称．△PAB中，PB∥y轴，AB∥x轴，PB与AB相交于点B．若△PAB的面积大于12，试判断关于x的方程（a-1）x2-x+
1
4
=0的根的情况．
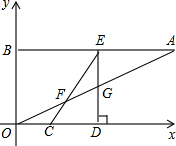如图，在平面直角坐标系xOy中，点A、B的坐标分别为（16，8）、（0，8），线段CD在x轴上，CD=6，点C从原点出发沿x轴正方向以每秒2个单位长度向右平移，点D随着点C同时同速同方向运动，过点D作x轴的垂线交线段AB于点E，交OA于点G，连接CE交OA于点F．设运动时间为t，当E点到达A点时，停止所有运动．
（1）求线段CE的长；
（2）记△CDE与△ABO公共部分的面积为S，求S关于t的函数关系式；
（3）连接DF．当t取何值时，以C、F、D为顶点的三角形为等腰三角形？
如图，在△ABC中，点D在BC上，BD=AD=AC，∠BAC=60°，求∠B的度数．
请阅读下列材料：
问题：如图①，将菱形ABCD和菱形BEFG拼接在一起，使得点A，B，E在同一条直线上，点G在BC边上，P是线段DF的中点，连接PG，PC．若∠ABC=120°，试探究PG与PC的位置关系及∠PCG的大小．小明同学的思路是：延长GP交DC于点H，构造全等三角形，经过推理使问题得到解决．请你参考小明的思路，探究并解决下列问题：
（1）直接写出上面问题中线段PG与PC的位置关系及∠PCG的大小；
（2）将图①中的菱形BEFG绕点B顺时针旋转，使点E恰好落在CB的延长线上，原问题中的其他条件不变（如图②）．你在（1）中得到的两个结论是否仍成立？写出你的猜想并加以证明．
如图，排球运动员站在点O处练习发球，将球从O点正上方1.8m的A处发出，把球看成点，其运行的高度y（m）与运行的水平距离x（m）满足关系式y=q（x-7）2+h．已知球网与O点的水平距离为9m，高度为2.24m，球场的边界距O点的水平距离为18m．

（1）当h=2.5时，求y与x的关系式（不要求写出自变量x的取值范围）
（2）当h=2.5时，球能否越过球网？球会不会出界？请说明理由；
（3）若球一定能越过球网，又不出边界，求a的取值范围．
已知三个连续奇数，其中最小的数的平方的三倍减去25和两个较大的数的平方和相等，试求这三个连续奇数．
甲、乙两个小队参加90公里的远足活动，甲队先步行，乙队乘汽车，两小队同地同时出发，汽车将乙队送到目的地后回头接甲队（汽车掉头时间忽略不计），若甲队每小时走5千米，汽车的速度是每小时45千米，那么甲队到目的地需要多长时间？
我们给出如下定义：如图1，平面内两直线l1、l2相交于点O，对于平面内的任意一点M，若p、q分别是点M到直线l1和l2的距离（p≥0，q≥0），我们称有序非负实数对[p，q]是点M的距离坐标．
根据上述定义请解答下列问题：
如图2，平面直角坐标系xOy中，直线l1的解析式为y=x，直线l2的解析式为y=
1
2
x，M是平面直角坐标系内的点，
（1）若p=q=0，求距离坐标为[0，0]时，点M的坐标；
（2）若q=0，且p+q=m（m＞0），利用图2，求距离坐标为[p，q]时，点M的坐标；
（3）若p=1，q=1，则坐标平面内距离坐标为[p，q]的时候，点M可以有几个位置？在图3中画出所有符合条件的点M（简要说明画法）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网