题目内容
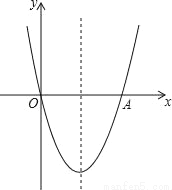
如图,抛物线y=x2﹣4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q.
(1)这条抛物线的对称轴是 ,直线PQ与x轴所夹锐角的度数是 ;
(2)若两个三角形面积满足S△POQ=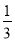 S△PAQ,求m的值;
S△PAQ,求m的值;
(3)当点P在x轴下方的抛物线上时,过点C(2,2)的直线AC与直线PQ交于点D,求:①PD+DQ的最大值;②PD•DQ的最大值.
练习册系列答案
相关题目
题目内容
如图,抛物线y=x2﹣4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q.
(1)这条抛物线的对称轴是 ,直线PQ与x轴所夹锐角的度数是 ;
(2)若两个三角形面积满足S△POQ=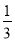 S△PAQ,求m的值;
S△PAQ,求m的值;
(3)当点P在x轴下方的抛物线上时,过点C(2,2)的直线AC与直线PQ交于点D,求:①PD+DQ的最大值;②PD•DQ的最大值.
