题目内容

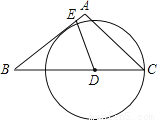
如图，在等腰△ABC中，AB=AC=5，BC=6，点D为BC边上一动点（不与点B重合），过D作射线DE交AB边于E，使∠BDE=∠A，以D为圆心、DC的长为半径作⊙D．

（1）设BD=x，AE=y，求y关于x的函数关系式，并写出定义域．

（2）当⊙D与AB边相切时，求BD的长．

（3）如果⊙E是以E为圆心，AE的长为半径的圆，那么当BD的长为多少时，⊙D与⊙E相切？

(1) y=5-x（0＜x≤）；(2) ；(3) 或． 【解析】 试题分析：（1）通过相似三角形△BDE∽△BAC的对应边成比例得到，把相关线段的长度代入并整理得到y=5-x（0＜x≤）； （2）如图，假设AB与⊙D相切于点F，连接FD．通过相似三角形△BFD∽△BGA的对应边成比例得到．DF=6-BD，由勾股定理求得AG=4，BA=5，所以把相关线段的长度代入便可以求得BD的长...
练习册系列答案
相关题目

如图，一宽为2cm的刻度尺在圆上移动，当刻度尺的一边与圆相切时，另一边与圆两个交点处的读数恰好为“2”和“8”（单位：cm），则该圆的半径为_____cm．

cm 【解析】试题分析：作OE垂直AB于E交⊙O与D，设OB=r，由垂径定理，BE=AB=3，由题意列方程得： ，解得：r=，∴该圆的半径为cm．故答案为：．

如图，抛物线y=x2﹣4x与x轴交于O，A两点，P为抛物线上一点，过点P的直线y=x+m与对称轴交于点Q．

（1）这条抛物线的对称轴是　 　，直线PQ与x轴所夹锐角的度数是　 　；

（2）若两个三角形面积满足S△POQ=S△PAQ，求m的值；

（3）当点P在x轴下方的抛物线上时，过点C（2，2）的直线AC与直线PQ交于点D，求：①PD+DQ的最大值；②PD•DQ的最大值．

（1）2，45°；（2）﹣1或2；（3）①6；②18. 【解析】试题分析：（1）把解析式转化成顶点式，或利用对称轴公式即可得该抛物线的对称轴，利用直线y=x+m与坐标轴的交点坐标即可求得直线PQ与x轴所夹锐角的度数；（2）分情况讨论，即直线PQ与x轴的交点落在OA的延长线上，OA上，AO的延长线上三种情况讨论m值.设直线PQ交x轴于点B，分别过O点，A点作PQ的垂线，垂足分别是E、F，，当点...

2﹣1等于__．

【解析】2﹣1=. 故答案为.

有一种细胞直径约为0.000 058cm．用科学记数法表示这个数为（　　）

A. 5.8×10﹣6 B. 5.8×10﹣5 C. 0.58×10﹣5 D. 58×10﹣6

B 【解析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10-n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定，0.000058=5.8×10-5 故选B

在一次环保知识测试中，三年一班的两名同学根据班级成绩（分数为整数）分别绘制了不同的频率分布直方图，如图1、2，已知图1从左到右每个小组的频率分别为0.04、0.08、0.24、0.32、0.20、0.12，其中68.5～76.5小组的频数为12；图2从左到右每个小组的频数之比为1：2：4：7：6：3：2，请结合条件和频率分布直方图回答下列问题：

（1）三年一班参加测试的人数是多少？

（2）若这次测试的成绩80分以上（含80分）为优秀，则优秀率是多少？

（3）若这次测试的成绩60分以上（含60分）为及格，则及格率是多少？

（1）50人（2）44％（3）96% 【解析】试题分析：（1）根据频率分布直方图知道68.5～76.5小组为第三小组，频率为0.24，频数为12，由此即可求出三年一班参加测试的人数； （2）根据图2从左到右每个小组的频数之比为1：2：4：7：6：3：2可以求出各个小组的频率，然后就可以找到这次测试的成绩80分以上（含80分）的人数，也就可以求出优秀率； （3）根据图1可以得到这次测试的成...

若0≤x≤3，则函数y=x2﹣2x﹣3的取值范围是_____．

﹣4≤y≤0 【解析】试题解析： ∴函数图象开口向上，对称轴为x=1，有最小值?4， ∴当x=3时，有最大值为0， ∴y的取值范围为： 故答案为：

已知在△ABC中,∠ACB=90°,CD⊥AB于D,BE:AB=3：5,若CE=， ，求tan∠AEC值及CD的长.

tan∠AEC=3, CD= 【解析】【解析】 在RT△ACD与RT△ABC中 ∵∠ABC+∠CAD=90°, ∠ACD+∠CAD=90°∴∠ABC=∠ACD, ∴cos∠ABC=cos∠ACD= 在RT△ABC中， 令BC=4k,AB=5k 则AC=3k 由 ,BE=3k 则CE=k,且CE= 则k=，AC=3 ∴RT△ACE中，tan∠AEC==3 ∵RT...

下列各式中，能用平方差公式计算的是（　　）

A. B.

C. D.

C 【解析】根据平方差公式（a+b）（a-b）=a2-b2，可知： A、两项相同，不符合平方差公式； B、D两项都不相同，不符合平方差公式； C、中的两项都是一项完全相同，另一项互为相反数，符合平方差公式． 故选：C．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网