Question

10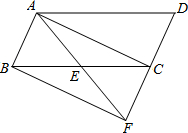．如图，在平行四边形ABCD中，E是BC的中点，连结AE并延长，交DC的延长线于点F．
（1）求证：△ABE≌△FCE；
（2）当∠ABF=90°时，∠AEC与∠D的数量关系是∠AEC=2∠D，并说明理由．

Answer 1

分析 （1）根据平行四边形的对边平行得到AB与DC平行，再根据两直线平行内错角相等得到一对角相等，由E为BC的中点，得到两条线段相等，再由对应角相等，利用ASA可得出△ABE与△FCE全等；
（2）首先利用矩形的判定与性质得出∠ABE+∠BAE=∠AEC，进而利用平行四边形的性质得出答案．

解答 （1）证明：∵四边形ABCD为平行四边形，
∴AB∥DC，
∴∠ABE=∠ECF，
又∵E为BC的中点，
∴BE=CE，
在△ABE和△FCE中，
∵$\left\{\begin{array}{l}{∠ABE=∠ECF}\\{BE=CE}\\{∠AEB=∠FEC}\end{array}\right.$，
∴△ABE≌△FCE（ASA）；

（2）∠AEC=2∠D，
理由：∵△ABE≌△FCE，
∴AE=EF，BE=EC，
∴四边形ABFC是平行四边形，
∵∠ABF=90°，
∴平行四边形ABFC是矩形，
∴AE=BE，
∴∠BAE=∠ABE，
∴∠ABE+∠BAE=∠AEC，
∵四边形ABCD为平行四边形，
∴∠ABE=∠D，
∴∠AEC=2∠D．
故答案为：∠AEC=2∠D．

点评 此题考查了矩形的判定、平行四边形的性质、以及全等三角形的判定与性质，熟练掌握判定与性质是解本题的关键．