题目内容
14.若$\frac{1}{2}$x2y+A=$\frac{1}{2}$xy(B+xy),则A=$\frac{1}{2}{x}^{2}{y}^{2}$,B=x.分析 根据单项式和多项式的乘法法则进行展开解答即可.
解答 解:因为:$\frac{1}{2}$xy(B+xy)=$\frac{1}{2}{x}^{2}{y}^{2}+\frac{1}{2}xyB$,
又因为$\frac{1}{2}$x2y+A=$\frac{1}{2}$xy(B+xy),
所以可得:B=x,A=$\frac{1}{2}{x}^{2}{y}^{2}$,
故答案为:$\frac{1}{2}{x}^{2}{y}^{2}$;x
点评 此题考查单项式和多项式的乘法,关键是根据法则进行计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.甲、乙、丙、丁四人进行射击测试,每人10次,射击成绩的平均数都是8.6环,方差分别是S甲2=0.45,S乙2=0.50,S丙2=0.55,S丁2=0.60,则射击成绩最稳定的是( )
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
6.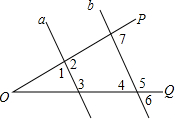 如图,已知直线a∥b,同时与∠POQ的两边相交,则下列结论中错误的是( )
如图,已知直线a∥b,同时与∠POQ的两边相交,则下列结论中错误的是( )
 如图,已知直线a∥b,同时与∠POQ的两边相交,则下列结论中错误的是( )
如图,已知直线a∥b,同时与∠POQ的两边相交,则下列结论中错误的是( )| A. | ∠3+∠4=180° | B. | ∠2+∠5>180° | C. | ∠1+∠6<180° | D. | ∠2+∠7=180° |
3.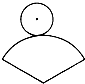 如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径为r,扇形的圆心角等于120°,则围成的圆锥模型的高为( )
如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径为r,扇形的圆心角等于120°,则围成的圆锥模型的高为( )
 如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径为r,扇形的圆心角等于120°,则围成的圆锥模型的高为( )
如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径为r,扇形的圆心角等于120°,则围成的圆锥模型的高为( )| A. | 2$\sqrt{2}$r | B. | r | C. | $\sqrt{10}$r | D. | 3r |
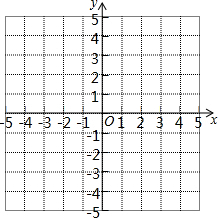 画出函数y=x-3的图象,并根据图象指出:
画出函数y=x-3的图象,并根据图象指出: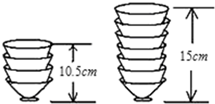 如图,两摞相同规格的饭碗整齐地叠放在桌面上,请根据图中给的数据信息,解答下列问题:
如图,两摞相同规格的饭碗整齐地叠放在桌面上,请根据图中给的数据信息,解答下列问题: